题目内容
5.如图,已知△ABC≌△CDA,将△ABC沿AC所在的直线折叠至△AB′C的位置,点B的对应点为B′,连结BB′.(1)直接填空:B′B与AC的位置关系是垂直;
(2)点P、Q分别是线段AC、BC上的两个动点(不与点A、B、C重合),已知△BB′C的面积为36,BC=8,求PB+PQ的最小值;
(3)试探索:△ABC的内角满足什么条件时,△AB′E是直角三角形?

分析 (1)根据翻折变换的性质得到AB=AB′,∠BAC=∠B′AC,根据等腰三角形的性质得到结论;
(2)根据三角形的面积公式求出△BB′C的BC边上的高,根据轴对称变换的性质解答;
(3)分∠AB′E=90°和∠AEB′=90°两种情况,根据翻折变换的性质和平行线的性质解答.
解答 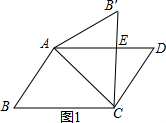 解:(1)由翻折变换的性质可知,AB=AB′,∠BAC=∠B′AC,
解:(1)由翻折变换的性质可知,AB=AB′,∠BAC=∠B′AC,
∴B′B⊥AC,
故答案为:垂直;
(2)∵AB=AB′,∠BAC=∠B′AC,
∴AC是B′B的垂直平分线,
∴点B′与点B关于直线AC轴对称,
连接B′Q,则B′Q是PB+PQ的最小值,
∵△BB′C的面积为36,BC=8,
∴△BB′C的BC边上的高为36×2÷8=9,
当B′Q⊥BC时,B′Q最小,
∴PB+PQ的最小值为9;
(3)①如图1,当∠ACB=45°时,∠AEB′=90°.
∵由翻折变换的性质可知,∠BCA=∠B′CA,
∴∠BCB′=90°,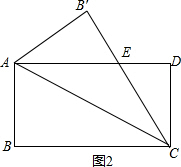
∵△ABC≌△CDA,
∴AB=CD,BC=AD,
∴四边形ABCD的平行四边形,
∴AD∥BC,
∴∠AEB′=∠BCB′=90°;
②如图2,由翻折变换的性质可知,当∠ABC=90°时,∠AB′E=90°.
点评 本题考查的是翻折变换的性质、轴对称-最短路径问题、等腰三角形的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
相关题目
17.下列各式中,不能用平方差公式计算的是( )
| A. | (-x+y)(x-y) | B. | (x2-2y2)(x2+2y2) | C. | (x+y-z)(-z-y+x) | D. | (2x-y)(-y-2x) |
15.下列事件是随机事件的是( )
| A. | 明天太阳从东方升起 | |
| B. | 射击运动员射击一次,命中靶心 | |
| C. | 通常条件下温度降到0℃,水结冰 | |
| D. | 任意画一个三角形,其内角和为360° |
 如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4).
如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4).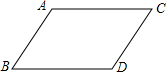 如图,将长为4cm的线段AB沿着点A到点C的方向平移6cm得到线段CD,那么四边形ABDC的周长是20cm.
如图,将长为4cm的线段AB沿着点A到点C的方向平移6cm得到线段CD,那么四边形ABDC的周长是20cm.