题目内容
16. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2$\sqrt{10}$,点H是BD上的一个动点,求HG+HC的最小值.
分析 (1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
解答 解:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
$\left\{\begin{array}{l}{∠EDF=∠GBF}\\{∠EFD=∠GFB}\\{DF=BF}\end{array}\right.$,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小, 在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2$\sqrt{10}$,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2$\sqrt{10}$,
∴EM=$\frac{1}{2}$BE=$\sqrt{10}$,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=$\sqrt{10}$,MN=DE=2$\sqrt{10}$,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=$\sqrt{10}$,
∴MC=3$\sqrt{10}$,
在RT△EMC中,∵∠EMC=90°,EM=$\sqrt{10}$.MC=3$\sqrt{10}$,
∴EC=$\sqrt{E{M}^{2}+M{C}^{2}}$=$\sqrt{(\sqrt{10})^{2}+(3\sqrt{10})^{2}}$=10.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识,解题的关键是利用对称找到点H的位置,属于中考常考题型.

| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165cm,165cm | B. | 165cm,170cm | C. | 170cm,165cm | D. | 170cm,170cm |
| A. | 此不等式组无解 | B. | 此不等式组有7个整数解 | ||
| C. | 此不等式组的负整数解是-3,-2,-1 | D. | 此不等式组的解集是-$\frac{5}{2}$<x≤2 |
 图中三视图对应的正三棱柱是( )
图中三视图对应的正三棱柱是( )| A. |  | B. |  | C. |  | D. |  |
| A. | ($\frac{1}{7}$,9$\frac{4}{7}$) | B. | ($\frac{1}{8}$,9$\frac{5}{8}$) | C. | ($\frac{1}{9}$,9$\frac{7}{9}$) | D. | ($\frac{1}{10}$,9$\frac{9}{10}$) |




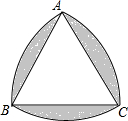 如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$.
如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$. 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.
如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.