题目内容
4．
如图，已知CA=CB，则数轴上点A所表示的数是1-$\sqrt{5}$．
分析 首先在直角三角形中，利用勾股定理可以求出线段CB的长度，得出CA的长度，求出点A与原点的距离，即可得出数轴上点A所表示的数．
解答 解：根据题意，由勾股定理得：CB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴CA=CB=$\sqrt{5}$，
∴A到原点的距离是 $\sqrt{5}$-1，
∵A在原点左侧，
∴点A所表示的数是1-$\sqrt{5}$，
故答案为：1-$\sqrt{5}$．
点评 此题主要考查了实数与数轴之间的对应关系、勾股定理；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．已知a、b、c是常数，且a≠0，则关于x的方程ax2+bx+c=0有实数根的条件是（ ）
| A． | b2-4ac＜0 | B． | b2-4ac＞0 | C． | b2-4ac≥0 | D． | b2-4ac≤0 |
12．若|a+2|+（b-1）2=0，那么代数式（a+b）2009的值是（ ）
| A． | 2009 | B． | -2009 | C． | 1 | D． | -1 |
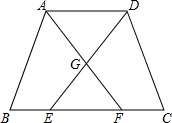如图，等腰梯形ABCD中，AD∥BC，点E、F在边BC上，且BE=CF，AF与DE相交于点G．求证：GE=GF．
14．下列多项式中能用平方差公式分解因式的是（ ）
| A． | a2+b2 | B． | 5m2-20mn | C． | -x2-y2 | D． | x2-9 |