题目内容
10.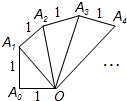 如图是由一系列直角三角形组成的螺旋形,OA=OA1=OA2=…OAn=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
如图是由一系列直角三角形组成的螺旋形,OA=OA1=OA2=…OAn=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
分析 这是一个规律性题目,第一个三角形的斜边正好是第二个三角形的直角边,依次进行下去,且有一个直角边的边长为1.从而可求出面积.
解答 解:根据题意可知:OA1=$\sqrt{2}$,OA2=$\sqrt{3}$,…
∴第n个直角三角形的直角边OAn-1长为$\sqrt{n}$.
∵第n个直角三角形的另一条直角边长为1.
∴第n个直角三角形的面积为$\frac{1}{2}$×1×$\sqrt{n}$=$\frac{\sqrt{n}}{2}$.
故答案为:$\frac{\sqrt{n}}{2}$.
点评 本题考查勾股定理的应用,应用勾股定理求出三角形的斜边正好是下一个三角形的直角边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 将n个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5,…是正方形对角线的交点,那么阴影部分面积之和等于$\frac{1}{4}$(n-1).
将n个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5,…是正方形对角线的交点,那么阴影部分面积之和等于$\frac{1}{4}$(n-1). 如图,一个60°角的三角形纸片,剪去这个60°角后,则∠1+∠2的度数为240°.
如图,一个60°角的三角形纸片,剪去这个60°角后,则∠1+∠2的度数为240°.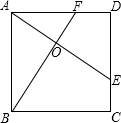 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..
 如图,将正方形ABCD的边BC延长到E,使CE=AC,AE与DC交于点F,则CE:FC=$\sqrt{2}$+1.
如图,将正方形ABCD的边BC延长到E,使CE=AC,AE与DC交于点F,则CE:FC=$\sqrt{2}$+1.