题目内容
19.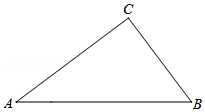 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设出发的时间为t秒
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设出发的时间为t秒(1)出发1秒后,△ABP的周长=(7+$\sqrt{13}$)cm,;
(2)当t=1.5s或2.7s时,△BCP是以BP为底边的等腰三角形;
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
分析 (1)根据速度为每秒2cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长.
(2)由勾股定理得AC=4cm,有两种情况,①当点P在边AC上时;②当点P在边AB上时;求出点P运动的路程,即可得出结果;.
(3)分类讨论:当P点在AC上,Q在BC上,则PC=2t,CQ=t,根据题意得出方程,解方程即可;当P点在BC上,Q在AB上,则BQ=t-3,BQ=2t-9;根据题意得出方程,解方程即可.
解答 解:(1)如图1所示: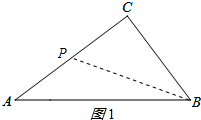
由∠C=90°,AB=5cm,BC=3cm,
∴AC=$\sqrt{{AB}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm),
动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2cm,∴AP=2cm,
∵∠C=90°,
∴PB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$(cm),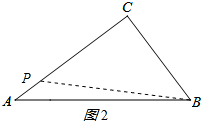
∴△ABP的周长为:AP+PB+AB=2+5+$\sqrt{13}$=7+$\sqrt{13}$(cm),
故答案为:(7+$\sqrt{13}$)cm,
(2)分两种情况:
①如图2所示:
当点P在边AC上时,CP=BC=3cm,3÷2=1.5(s),
此时用的时间为1.5s,△BCP是以BP为底边的等腰三角形;
②如图3所示: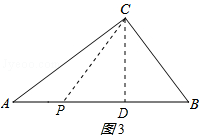
当点P在边AB上时,CP=BC=3cm,
过C作斜边AB的高CD,则CD=$\frac{3×4}{5}$=2.4(cm),
在Rt△PCD中,PD=$\sqrt{P{C}^{2}-C{D}^{2}}$=$\sqrt{{3}^{2}-2.{4}^{2}}$=1.8(cm),
∴BP=2PD=3.6cm,
所以P运动的路程为9-3.6=5.4(cm),
则用的时间为5.4÷2=2.7(s),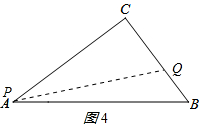 △BCP为等腰三角形;
△BCP为等腰三角形;
综上所述:当t=1.5s或2.7s 时,△BCP是以BP为底边的等腰三角形;
故答案为:1.5s或2.7s;
(3)分两种情况:
①如图6所示:
当P点在AC上,Q在BC上,则PC=2t,CQ=t,
∵直线PQ把△ABC的周长分成相等的两部分,
∴2t+t=4-2t+3-t+5,
解得:t=2;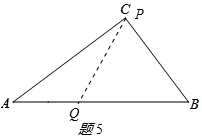
②如图7所示:
当P点在BC上,Q在AB上,则BQ=t-3,BQ=2t-9
∴AQ=5-(t-3)=8-t,CQ=3-(2t-9)=12-2t,
∵直线PQ把△ABC的周长分成相等的两部分,
∴4+8-t+12-2t=t-3+2t-9,
解得:t=6,
综上所述:当t为2s或6s时,直线PQ把△ABC的周长分成相等的两部分.
点评 此题考查了勾股定理、等腰三角形的判定与性质以及三角形面积的计算;此题涉及到了动点,有一定难度,熟练掌握等腰三角形的判定与性质和勾股定理,进行分类讨论是解决问题的关键.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案| A. | 32与43 | B. | 3c2b与-8b2c | C. | xy与4xyz | D. | 4mn2与2m2n |
| A. | 4 | B. | 2 | C. | ±4 | D. | ±2 |

 如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E.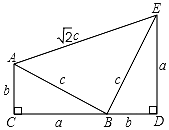 如图四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BDE的三边长,易知AE=$\sqrt{2}$c,这时我们把形如ax2+$\sqrt{2}$cx+b=0的方程称为关于x的“勾系一元二次方程”,请解决下列问题:
如图四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BDE的三边长,易知AE=$\sqrt{2}$c,这时我们把形如ax2+$\sqrt{2}$cx+b=0的方程称为关于x的“勾系一元二次方程”,请解决下列问题: