题目内容
8.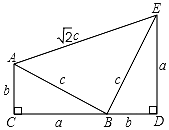 如图四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BDE的三边长,易知AE=$\sqrt{2}$c,这时我们把形如ax2+$\sqrt{2}$cx+b=0的方程称为关于x的“勾系一元二次方程”,请解决下列问题:
如图四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BDE的三边长,易知AE=$\sqrt{2}$c,这时我们把形如ax2+$\sqrt{2}$cx+b=0的方程称为关于x的“勾系一元二次方程”,请解决下列问题:(1)写出一个“勾系一元二次方程”;
(2)证明:关于x的“勾系一元二次方程”ax2+$\sqrt{2}$cx+b=0必有实数根.
分析 (1)直接找一组勾股数代入方程即可;
(2)通过判断根的判别式△的正负来证明结论.
解答 解:(1)当a=3,b=4,c=5时,
勾系一元二次方程为3x2+5$\sqrt{2}$x+4=0;
(2)证明:根据题意,得
△=($\sqrt{2}$c)2-4ab=2c2-4ab
∵a2+b2=c2
∴2c2-4ab=2(a2+b2)-4ab=2(a-b)2≥0
即△≥0
∴勾系一元二次方程ax2+$\sqrt{2}$cx+b=0必有实数根.
点评 此类题目要读懂题意,根据题目中所给的材料结合勾股定理和根的判别式解题.

练习册系列答案
相关题目
18.抛物线y=(x+3)2-4可以由抛物线y=x2平移得到,则下列平移过程正确的是( )
| A. | 先向左平移3个单位,再向上平移4个单位 | |
| B. | 先向左平移3个单位,再向下平移4个单位 | |
| C. | 先向右平移3个单位,再向下平移4个单位 | |
| D. | 先向右平移3个单位,再向上平移4个单位 |
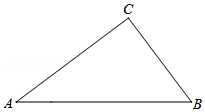 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设出发的时间为t秒
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设出发的时间为t秒
 如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为42°.
如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为42°.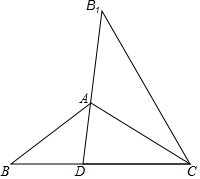 如图,在△ABC中,AB=AC,∠BAC=108°,将△ABC沿直线AC翻折得△AB1C,延长B1A交BC于D,求证:点B1在CD的垂直平分线上.
如图,在△ABC中,AB=AC,∠BAC=108°,将△ABC沿直线AC翻折得△AB1C,延长B1A交BC于D,求证:点B1在CD的垂直平分线上.