题目内容
20.先化简,再求值:$\frac{{{x^2}-1}}{{{x^2}+x}}÷(\frac{{{x^2}+1}}{x}-2),其中x=\sqrt{3}+1$.分析 先化简原式,然后将x的值代入即可求出答案.
解答 解:原式=$\frac{(x-1)(x+1)}{x(x+1)}$÷$\frac{{x}^{2}-2x+1}{x}$
=$\frac{x-1}{x}$×$\frac{x}{(x-1)^{2}}$
=$\frac{1}{x-1}$
当x=$\sqrt{3}$+1时,
∴原式=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.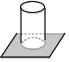 如图,一个放置在水平桌面上的圆柱,从正面看到的图形是( )
如图,一个放置在水平桌面上的圆柱,从正面看到的图形是( )
 如图,一个放置在水平桌面上的圆柱,从正面看到的图形是( )
如图,一个放置在水平桌面上的圆柱,从正面看到的图形是( )| A. |  | B. |  | C. |  | D. |  |
 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠BDC的度数是30°.
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠BDC的度数是30°.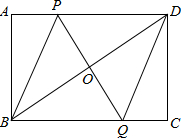 如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.