题目内容
11. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠BDC的度数是30°.
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠BDC的度数是30°.
分析 由旋转的性质知∠AOD=30°,OA=OD,根据等腰三角形的性质及三角形内角和定理,可得∠ADO、∠ODC的度数,进而得出∠BDC的度数.
解答 解:由旋转得,∠AOD=30°,OA=OD,
∴∠A=∠ADO=(180°-30°)÷2=75°,
由旋转可得∠ODC=∠A=75°,
∴∠BDC=180°-75°×2=30°,
故答案为:30°.
点评 本题主要考查了旋转的性质的运用,解决问题的关键是掌握:旋转前、后的图形全等.本题也可以根据∠BDC=∠BOC得出结论.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16.投掷一枚质地均匀的骰子一次,正面是偶数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
1.下面计算正确的是( )
| A. | 4a-3a=1 | B. | a2+a3=a5 | C. | x6÷x3=x2 | D. | (-2a3)2=4a6 |
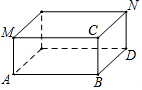 如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.
如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.