题目内容
15.对于二次函数y=-x2+2x有下列四个结论:①它的对称轴是直线x=1;
②设y1=-x12+2x1,y2=-x22+2x2,则当x2>x1>0时,有y1>y2;
③它的图象与x轴的两个交点是(0,0)和(2,0);
④直线y=k与y=-x2+2x的图象有两个不同的交点,则k<1;
其中正确结论的个数为3.
分析 利用配方法求出二次函数对称轴,再求出图象与x轴交点坐标,进而结合二次函数性质得出答案.
解答 解:①y=-x2+2x=-(x-1)2+1,故它的对称轴是直线x=1,正确;
②∵直线x=1两旁部分增减性不一样,∴设y1=-x12+2x1,y2=-x22+2x2,则当x2>x1>0时,有y2>y1或y2<y1,错误;
③当y=0,则x(-x+2)=0,解得:x1=0,x2=2,
故它的图象与x轴的两个交点是(0,0)和(2,0),正确;
④∵直线y=k与y=-x2+2x的图象有两个不同的交点,
∴方程x2-2x+k=0的△=4-4k>0,
∴k<1,正确.
故正确结论有①③④,
故答案为3.
点评 此题主要考查了二次函数的性质以及一元二次方程的解法,得出抛物线的对称轴和其交点坐标是解题关键.

练习册系列答案
相关题目
1. 如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )
如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )
 如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )
如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )| A. | 20° | B. | 40° | C. | 50° | D. | 80° |
7.下表是小明填写实习报告的部分内容:已知:sin47°=0.7313,cos47°=0.6820,tan47°=1.0724,$\frac{1}{{tan{{47}°}}}$=0.9325,根据以上的条件,计算出铁塔顶端到山底的高度( )
| 题目 | 在山脚下测量铁塔顶端到山底的高度 | |
| 测量 目标 图示 |  | 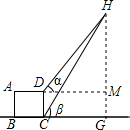 |
| CD=5m | ∠α=45°,∠β=47° | |
| A. | 64.87m | B. | 74.07m | C. | 84.08m | D. | 88.78m |
5.如果9a2-ka+4是完全平方式,那么k的值是( )
| A. | -12 | B. | 6 | C. | ±12 | D. | ±6 |
 在Rt△ABC中,∠C=90°,∠A<∠B,AM=BM=CM,沿CM将三角形AMC翻折,点A落在点D,CD⊥AB,则∠A=30度.
在Rt△ABC中,∠C=90°,∠A<∠B,AM=BM=CM,沿CM将三角形AMC翻折,点A落在点D,CD⊥AB,则∠A=30度.