题目内容
20.在每个小正方形的边长为1的网格中.点A,B,C,D均在格点上,点E、F分别为线段BC、DB上的动点,且BE=DF.(Ⅰ)如图①,当BE=$\frac{5}{2}$时,计算AE+AF的值等于$\frac{5+\sqrt{61}}{2}$
(Ⅱ)当AE+AF取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段AE,AF,并简要说明点E和点F的位置如何找到的(不要求证明)取格点H,K,连接BH,CK,相交于点P,连接AP,与BC相交,得点E,取格点M,N连接DM,CN,相交于点G,连接AG,与BD相交,得点F,线段AE,AF即为所求..
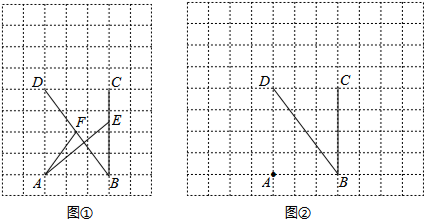
分析 (1)根据勾股定理得出DB=5,进而得出AF=2.5,由勾股定理得出AE=$\sqrt{{3}^{2}+2.{5}^{2}}=\frac{\sqrt{61}}{2}$,再解答即可;
(2)首先确定E点,要使AE+AF最小,根据三角形两边之和大于第三边可知,需要将AF移到AE的延长线上,因此可以构造全等三角形,首先选择格点H使∠HBC=∠ADB,其次需要构造长度BP使BP=AD=4,根据勾股定理可知BH=$\sqrt{{3}^{2}+{4}^{2}}$=5,结合相似三角形选出格点K,根据$\frac{HK}{BC}=\frac{HP}{BP}=\frac{1}{4}$,得BP=$\frac{4}{5}$BH=$\frac{4}{5}×5$=4=DA,易证△ADF≌△PBE,因此可得到PE=AF,线段AP即为所求的AE+AF的最小值;同理可确定F点,因为AB⊥BC,因此首先确定格点M使DM⊥DB,其次确定格点G使DG=AB=3,此时需要先确定格点N,同样根据相似三角形性质得到$\frac{NM}{DC}=\frac{MG}{DG}=\frac{2}{3}$,得DG=$\frac{3}{5}$DM=$\frac{3}{5}$×5=3,易证△DFG≌△BEA,因此可得到AE=GF,故线段AG即为所求的AE+AF的最小值.
解答 解:(1)根据勾股定理可得:DB=$\sqrt{{4}^{2}+{3}^{2}}=5$,
因为BE=DF=$\frac{5}{2}$,
所以可得AF=$\frac{1}{2}BD$=2.5,
根据勾股定理可得:AE=$\sqrt{{3}^{2}+2.{5}^{2}}=\frac{\sqrt{61}}{2}$,所以AE+AF=$2.5+\frac{\sqrt{61}}{2}=\frac{5+\sqrt{61}}{2}$,
故答案为:$\frac{5+\sqrt{61}}{2}$;
(2)如图,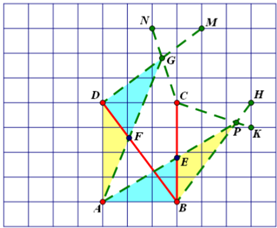
首先确定E点,要使AE+AF最小,根据三角形两边之和大于第三边可知,需要将AF移到AE的延长线上,因此可以构造全等三角形,首先选择格点H使∠HBC=∠ADB,其次需要构造长度BP使BP=AD=4,根据勾股定理可知BH=$\sqrt{{3}^{2}+{4}^{2}}$=5,结合相似三角形选出格点K,根据$\frac{HK}{BC}=\frac{HP}{BP}=\frac{1}{4}$,得BP=$\frac{4}{5}$BH=$\frac{4}{5}×5$=4=DA,易证△ADF≌△PBE,因此可得到PE=AF,线段AP即为所求的AE+AF的最小值;同理可确定F点,因为AB⊥BC,因此首先确定格点M使DM⊥DB,其次确定格点G使DG=AB=3,此时需要先确定格点N,同样根据相似三角形性质得到$\frac{NM}{DC}=\frac{MG}{DG}=\frac{2}{3}$,得DG=$\frac{3}{5}$DM=$\frac{3}{5}$×5=3,易证△DFG≌△BEA,因此可得到AE=GF,故线段AG即为所求的AE+AF的最小值.
故答案为:取格点H,K,连接BH,CK,相交于点P,连接AP,与BC相交,得点E,取格点M,N连接DM,CN,相交于点G,连接AG,与BD相交,得点F,线段AE,AF即为所求.
点评 此题考查最短路径问题,关键是根据轴对称的性质进行分析解答.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案| A. |  | B. |  | C. |  | D. |  |
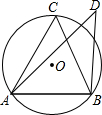 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
| A. |  | B. |  | C. |  | D. |  |
 阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:
阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
(1)前10株西红柿秧上小西红柿个数的平均数是47,中位数是49.5,众数是60;
(2)若对这20个数按组距为8进行分组,请补全频数分布表及频数分布直方图
| 个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
| 频数 | 2 | 5 | 7 | 4 | 2 |
 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
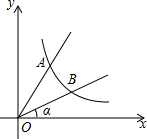 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=$\frac{1}{2}$.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=$\frac{1}{2}$. 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.