题目内容
18.如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C1;把△绕点C顺时针旋转180°,得到△CP2D.依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )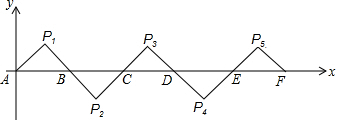
| A. | (4030,1) | B. | (4029,-1) | C. | (4033,1) | D. | (4031,-1) |
分析 根据等腰直角三角形的性质可找出点P1的坐标,结合旋转的性质即可找出点P2、P3、P4、P5、…、的坐标,根据坐标的变化即可找出变化规律“P2n+1(4n+1,1),P2n+2(4n+3,-1)(n为自然数)”,依此规律即可得出结论.
解答 解:∵A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,
∴P1(1,1).
∵把△AP1B绕点B顺时针旋转180°,得到△BP2C1,
∴P2(3,-1).
同理可得出:P3(5,1),P4(7,-1),P5(9,1),…,
∴P2n+1(4n+1,1),P2n+2(4n+3,-1)(n为自然数).
∵2017=2×1008+1,
∴P2017(4033,1).
故选C.
点评 本题考查了等腰直角三角形的性质、坐标与图形变化中的旋转以及规律型中点的坐标,根据点的变化找出变化规律“P2n+1(4n+1,1),P2n+2(4n+3,-1)(n为自然数)”是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
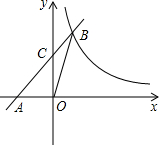 如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{3}{x}$在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<$\frac{3}{x}$的解集是0<x<1.其中正确的有( )
如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{3}{x}$在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<$\frac{3}{x}$的解集是0<x<1.其中正确的有( )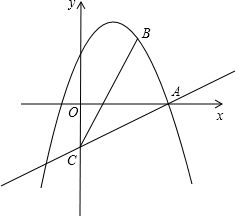 如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=$\frac{1}{3}$.
如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=$\frac{1}{3}$.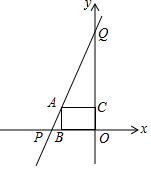 如图,直线y=2x+6与坐标轴分别交于P,Q两点,过函数图象上的点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,直线y=2x+6与坐标轴分别交于P,Q两点,过函数图象上的点A分别作两坐标轴的垂线,垂足分别为B,C.