题目内容
8.已知AB为⊙O的直径,DC与⊙O相切于点C,AD交⊙O于E点,$\widehat{EC}$=$\widehat{CB}$.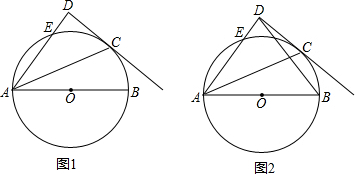
(1)如图1,求证:AD⊥DC.
(2)如图2,连接BD,若CD=12,AD=16,求tan∠ADB的值.
分析 (1)连接OC,如图1,利用$\widehat{EC}$=$\widehat{CB}$得到∠1=∠2,再证明OC∥AD,然后根据切线的性质得到OC⊥AD,于是可判断AD⊥DC;
(2)接BE、OC,它们相交于点H,如图2,利用垂径定理的推论,由$\widehat{EC}$=$\widehat{CB}$得到OC⊥BE,EH=BH,再证明四边形CDEH为矩形得到EH=CD=12,DE=CH,设DE=x,⊙O的半径为r,则AE=AD-DE=16-x,OH=r-x,根据三角形中位线性质的∴6-x=2(r-x),r=$\frac{1}{2}$(16+x),则AB=16+x,接着利用勾股定理得到(16-x)2+242=(16+x)2,解得x=9,然后根据正切的定义求解.
解答 (1)证明:连接OC,如图1,
∵$\widehat{EC}$=$\widehat{CB}$,
∴∠1=∠2,
∵OA=OC,
∴∠1=∠3,
∴∠2=∠3,
∴OC∥AD,
∵DC与⊙O相切于点C,
∴OC⊥AD,
∴AD⊥DC;
(2)解:连接BE、OC,它们相交于点H,如图2,
∵$\widehat{EC}$=$\widehat{CB}$,
∴OC⊥BE,EH=BH,
∵OC⊥AD,AD⊥DC,
∴四边形CDEH为矩形,
∴EH=CD=12,DE=CH,
∴BE=2EH=24,
设DE=x,⊙O的半径为r,则AE=AD-DE=16-x,OH=r-x,
而AE=2OH,
∴16-x=2(r-x),
∴r=$\frac{1}{2}$(16+x),
∴AB=16+x,
在Rt△ABE中,(16-x)2+242=(16+x)2,解得x=9,
∴tanEDB=$\frac{BE}{DE}$=$\frac{24}{9}$=$\frac{8}{3}$,
即tan∠ADB的值为$\frac{8}{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了解直角三角形.

| A. | (4030,1) | B. | (4029,-1) | C. | (4033,1) | D. | (4031,-1) |
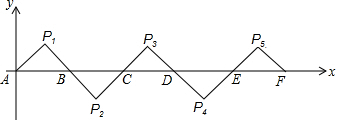
 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )| A. | (1345,0) | B. | (1345,$\frac{\sqrt{3}}{2}$) | C. | (1345.5,0) | D. | (1345.5,$\frac{\sqrt{3}}{2}$) |
| A. | 了解某路口每天在学校放学时段的车流量 | |
| B. | 检测某种新型LED灯的使用寿命 | |
| C. | 检测站对本市所有公交车的年度安全检查 | |
| D. | 了解同一批青菜的农药残留量 |
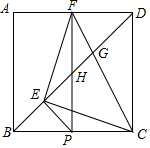 如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
 已知A(0,8),B(6,0),在坐标轴上取一点P,使三角形ABP为等腰三角形,求P点的坐标.
已知A(0,8),B(6,0),在坐标轴上取一点P,使三角形ABP为等腰三角形,求P点的坐标.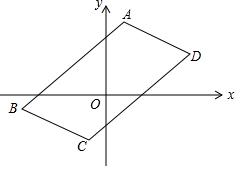 图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点
图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点 画出函数y=$\frac{6}{x}$(x>0)的图象.
画出函数y=$\frac{6}{x}$(x>0)的图象.