题目内容
已知x1,x2是关于x的方程x2-2x-a=0的两个实数根,且x1+2x2=3-
,则a= .
| 2 |
考点:根与系数的关系
专题:
分析:根据x1,x2是关于x的方程x2-2x-a=0的两个实数根,得出x1+x2=2,求出x2的值,由此求得方程的解,把方程的解代入原方程可以得到关于a是方程,通过解该方程即可求得a的值.
解答:解:∵x1,x2是关于x的方程x2-2x-a=0的两个实数根,
∴x1+x2=2,
∵x1+2x2=3-
,
∴2+x2=3-
,
∴x2=1-
,
∴(1-
)2-2(1-
)-a=0,
解得a=1.
故答案为:1.
∴x1+x2=2,
∵x1+2x2=3-
| 2 |
∴2+x2=3-
| 2 |
∴x2=1-
| 2 |
∴(1-
| 2 |
| 2 |
解得a=1.
故答案为:1.
点评:本题考查了根与系数的关系,x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据 如图,O是直线AB上一点,∠BOC=3∠AOC,OC是∠AOD的平分线.
如图,O是直线AB上一点,∠BOC=3∠AOC,OC是∠AOD的平分线.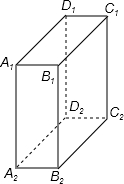 如图,有一个长宽高分别为2cm,1cm,3cm的长方体,有一只小蚂蚁想从点A2爬到点C1处,则它爬行的最短路程为
如图,有一个长宽高分别为2cm,1cm,3cm的长方体,有一只小蚂蚁想从点A2爬到点C1处,则它爬行的最短路程为