题目内容
 中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:几何图形问题
分析:过点C作CE⊥AB交AB延长线于E,设CE=x,在Rt△BCE和Rt△ACE中分别用x表示BE和AE的长度,然后根据AB+BE=AE,列出方程求出x的值,继而可判断“蛟龙”号能在保证安全的情况下打捞海底黑匣子.
解答: 解:过点C作CE⊥AB交AB延长线于E,
解:过点C作CE⊥AB交AB延长线于E,
设CE=x,
在Rt△BCE中,∵∠CBE=45°,
∴BE=CE=x,
在Rt△ACE中,∵∠CAE=30°,
∴AE=
x,
∵AB+BE=AE,
∴3000+x=
x,
解得:x=1500(
+1)≈4098(米),
显然2000+4098=6098<7062.68,
所以“蛟龙”号能在保证安全的情况下打捞海底黑匣子.
 解:过点C作CE⊥AB交AB延长线于E,
解:过点C作CE⊥AB交AB延长线于E,设CE=x,
在Rt△BCE中,∵∠CBE=45°,
∴BE=CE=x,
在Rt△ACE中,∵∠CAE=30°,
∴AE=
| 3 |
∵AB+BE=AE,
∴3000+x=
| 3 |
解得:x=1500(
| 3 |
显然2000+4098=6098<7062.68,
所以“蛟龙”号能在保证安全的情况下打捞海底黑匣子.
点评:本题考查俯角的定义,以及解直角三角形的实际应用问题.此题难度不大,解题的关键是要求学生能借助俯角构造直角三角形并解直角三角形,注意当两个直角三角形有公共边时,利用这条公共边进行求解是解此类题的常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
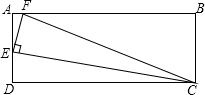 矩形ABCD中,AB=3AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
矩形ABCD中,AB=3AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.