题目内容
18.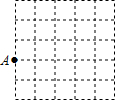 如图,在5×5的正方形网格中,设每个小正方形的边长都为1.已知点A在格点上(即小正方形的顶点).请你按下列要求完成问题:
如图,在5×5的正方形网格中,设每个小正方形的边长都为1.已知点A在格点上(即小正方形的顶点).请你按下列要求完成问题:(1)画一条线段AB,使得AB=$\sqrt{10}$,且点B在格点上;
(2)以上题中所画的线段AB为一边,画一个直角三角形△ABC,使点C在格点上,且另外两边长都是无理数;
(3)所画的△ABC的周长为2$\sqrt{5}$+$\sqrt{10}$(直接写出答案).
分析 (1)根据勾股定理画出线段AB即可;
(2)画出符合条件的△ABC即可;
(3)求出三角形各边的长,进而可得出结论.
解答  解:(1)点B 即为所求;
解:(1)点B 即为所求;
(2)如图,△ABC即为所求;
(3)∵AB=$\sqrt{10}$,BC=AC=$\sqrt{5}$,
∴△ABC的周长=2$\sqrt{5}$+$\sqrt{10}$.
故答案为:2$\sqrt{5}$+$\sqrt{10}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目

 AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°.
AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°.