题目内容
9.计算:(1)(-3)2+$\sqrt{12}$×(-$\sqrt{3}$)+($\sqrt{2}$)0
(2)(2$\sqrt{3}$+3$\sqrt{2}$)2-(2$\sqrt{3}$-3$\sqrt{2}$)2
(3)$\sqrt{72}$-($\sqrt{18}$-$\frac{2}{\sqrt{2}}$)
(4)$\frac{\sqrt{20}-4}{\sqrt{5}}$-$\sqrt{\frac{1}{5}}$.
分析 (1)利用二次根式的乘法法则和零指数幂的意义计算;
(2)利用完全平方公式计算;
(3)先把各二次根式化简为最简二次根式,然后合并即可;
(4)先进行二次根式的除法法则运算,然后化简后合并即可.
解答 解:(1)原式=9+2$\sqrt{3}$×(-$\sqrt{3}$)+1
=9-6+1
=4;
(2)原式=12+12$\sqrt{6}$+18-(12-18$\sqrt{6}$+18)
=24$\sqrt{6}$;
(3)原式=6$\sqrt{2}$-3$\sqrt{2}$+$\sqrt{2}$
=4$\sqrt{2}$;
(4)原式=2-$\frac{4\sqrt{5}}{5}$-$\frac{\sqrt{5}}{5}$
=2-$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
4.平行四边形ABCD是正方形需增加的条件是( )
| A. | 邻边相等 | B. | 邻角相等 | ||
| C. | 对角线互相垂直 | D. | 对角线互相垂直且相等 |
14.若(x-1)2+$\sqrt{x+y}$=0,则x2016+y2017的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
 如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,求S△ABC.
如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,求S△ABC.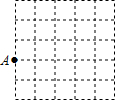 如图,在5×5的正方形网格中,设每个小正方形的边长都为1.已知点A在格点上(即小正方形的顶点).请你按下列要求完成问题:
如图,在5×5的正方形网格中,设每个小正方形的边长都为1.已知点A在格点上(即小正方形的顶点).请你按下列要求完成问题: 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C-A-B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C-A-B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).