题目内容
6.若c为正整数,且a+b=c,b+c=d,d+a=b,则(a+b)(b+c)(c+d)(d+a)的最小值为24.分析 将a+b=c,b+c=d,d+a=b利用等式的基本性质变形成a=-c、b=2c、d=3c,从而得(a+b)(b+c)(c+d)(d+a)=24c4,根据c为正整数即c最小为1可得答案.
解答 解:a+b=c ①,b+c=d ②,d+a=b ③,
由③得:b-a=d ④,
由②-④得:c+a=0,a=-c ⑤,
把⑤代入①得:-c+b=c,b=2c ⑥,
把⑥代入②得:2c+c=d,d=3c,
∵c为正整数,
∴c最小为1.
∴(a+b)(b+c)(c+d)(d+a)
=(-c+2c)(2c+c)(c+3c)(3c-c)
=(-1+2)×(2+1)×(1+3)×(3-1)
=24,
即(a+b)(b+c)(c+d)(d+a)的最小值为24,
故答案为:24.
点评 本题主要考查有理数的运算、等式的基本性质,根据已知等式变形成a、b、d全部用同一个字母c来表示是解题的关键.

练习册系列答案
相关题目
16.分式$\frac{6c}{{a}^{2}b}$与$\frac{c}{3a{b}^{2}}$的最简公分母是( )
| A. | ab | B. | 3ab | C. | 3a2b2 | D. | 3a2b6 |
 如图,在△ABC中,P是BC上一点,且∠APC<90°,以AP为一边作正方形APMN,若NC⊥BC,求∠ACB的度数.
如图,在△ABC中,P是BC上一点,且∠APC<90°,以AP为一边作正方形APMN,若NC⊥BC,求∠ACB的度数.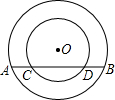 如图,在同心⊙O中,大圆的半径为5,大圆的弦AB与小圆交于CD,AB=8,CD=3.
如图,在同心⊙O中,大圆的半径为5,大圆的弦AB与小圆交于CD,AB=8,CD=3. 已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别6cm2和15cm2,则正方形③的面积为21cm2.
已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别6cm2和15cm2,则正方形③的面积为21cm2. 如图所示,一棵8米高的笔直的杉树在台风中被刮断,树顶C落在离树根B点4米处,科研人员要查看断痕A处的情况,在离树根B点1米的D处竖起一个梯子AD(点D、B、C在同一直线上),请问:这个梯子有多长?(结果请保留根号)
如图所示,一棵8米高的笔直的杉树在台风中被刮断,树顶C落在离树根B点4米处,科研人员要查看断痕A处的情况,在离树根B点1米的D处竖起一个梯子AD(点D、B、C在同一直线上),请问:这个梯子有多长?(结果请保留根号)