题目内容
10．下列实数是无理数的是（ ）| A． | -1 | B． | 0 | C． | $\sqrt{3}$ | D． | $\frac{1}{3}$ |
分析 由于无理数就是无限不循环小数，利用无理数的概念即可判定选择项．
解答 解：A、不是无理数，故本选项错误；
B、不是无理数，故本选项错误；
C、是无理数，故本选项正确；
D、不是无理数，故本选项错误；
故选C．
点评 此题主要考查了无理数定义．初中范围内学习的无理数有三类：①π类，如2π等；②开方开不尽的数，如$\sqrt{2}$等；③虽有规律但是无限不循环的数，如0.1010010001…，等．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
20．下列说法中正确的是（ ）
| A． | 单项式5xyz的次数是1 | B． | 单项式-$\frac{ab}{3}$的系数是-3 | ||
| C． | 多项式x-4的常数项是4 | D． | 多项式a2b-2a5+b4是五次三项式 |
18．
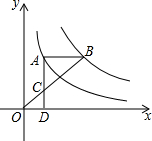如图，点A在双曲线y=$\frac{3}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，过点A作AD⊥x轴于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为（ ）
如图，点A在双曲线y=$\frac{3}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，过点A作AD⊥x轴于D．连接OB，与AD相交于点C，若AC=2CD，则k的值为（ ）| A． | 6 | B． | 9 | C． | 10 | D． | 12 |
15．
如图，OP=1，过P作PP1⊥OP且PP1=1，得OP1=$\sqrt{2}$；再过P1作P1P2⊥OP1且P1P2=1，得OP2=$\sqrt{3}$；又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1，得OP3=2，；…依次法继续作下去，则OP2015长为（ ）
如图，OP=1，过P作PP1⊥OP且PP1=1，得OP1=$\sqrt{2}$；再过P1作P1P2⊥OP1且P1P2=1，得OP2=$\sqrt{3}$；又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1，得OP3=2，；…依次法继续作下去，则OP2015长为（ ）| A． | 2015 | B． | 2016 | C． | $\sqrt{2015}$ | D． | $\sqrt{2016}$ |
已知依次函数y=x+1．
19．以下列长度的线段为边能构成直角三角形的是（ ）
| A． | 1，2，3 | B． | 6，8，12 | C． | 5，12，5 | D． | 7，24，25 |
20．
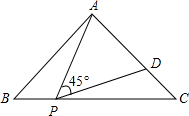如图，等腰直角△ABC的直角边长为3，P为斜边BC上的一点，且BP=1，D为AC上一点，若∠APD=45度，则以PA为边的正方形的面积为（ ）
如图，等腰直角△ABC的直角边长为3，P为斜边BC上的一点，且BP=1，D为AC上一点，若∠APD=45度，则以PA为边的正方形的面积为（ ）| A． | 10-3$\sqrt{2}$ | B． | 10-2$\sqrt{3}$ | C． | 4 | D． | 6 |