题目内容
6．
如图，AB为⊙O的直径，弦CD⊥AB于点E，若CD=8，且AE：BE=1：4，则AB的长度为（ ）| A． | 10 | B． | 5 | C． | 12 | D． | 5$\sqrt{3}$ |
分析 连接OC，设AE=x，表示出半径，在Rt△OCE中，用勾股定理得出x的值，从而得出AB的长．
解答 
解：连接OC，设AE=x，
∵AE：BE=1：4，
∴BE=4x，
∴OC=2.5x，
∴OE=1.5x，
∵CD⊥AB，
∴CE=DE，
∵CD=8，
∴CE=4，
Rt△OCE中，OE2+CE2=OC2，
∴（1.5x）2+42=（2.5x）2，
∴x=2，
∴AB=10，
故选A．
点评 本题考查了勾股定理以及垂径定理，掌握勾股定理以及垂径定理的用法是解题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
17．运用等式性质进行变形，不一定正确的是（ ）
| A． | 如果a=b，那么a+c=b+c | B． | 如果a=b，那么ac=bc | ||
| C． | 如果a+c=b+c，那么a=b | D． | 如果ac=bc，那么a=b |
14．若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=k，则k的值为（ ）
| A． | 2 | B． | -1 | C． | 2或-1 | D． | -2或1 |
1．抛物线y=2（x-3）2+1的顶点坐标是（ ）
| A． | （3，1） | B． | （4，-1） | C． | （-3，1） | D． | （-3，-1） |
11．已知$\frac{x+5}{16}$是一个最简真分数，那么x可以取的自然数有（ ）个．
| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
18．已知（x-6）（x-p）=x2+mx+36，那么m，p的值分别为（ ）
| A． | 12，6 | B． | -12，6 | C． | 12，-6 | D． | -12，-6 |
15．一项工程甲独做需10天完成，乙的工作效率是甲的2倍，两人合作了2天未完成，剩下的工作由乙完成，还需的天数为（ ）
| A． | 1天 | B． | 2天 | C． | 3天 | D． | 4天 |
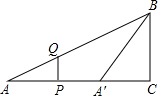如图，在Rt△ABC中，∠C=90°，AC=4，BC=2，P、Q分别是AC、AB边上的动点，PQ∥BC，点A关于直线PQ的对称点为A′，连结A′B，设线段AP的长为t．