题目内容
14.若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=k,则k的值为( )| A. | 2 | B. | -1 | C. | 2或-1 | D. | -2或1 |
分析 分①a+b+c=0时,用c表示出a+b,然后求解,②a+b+c≠0时,利用等比性质列式计算即可得解.
解答 解:①a+b+c=0时,a+b=-c,
所以,k=$\frac{a+b}{c}$=$\frac{-c}{c}$=-1;
②a+b+c≠0时,$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{c+a}{b}$=$\frac{a+b+b+c+c+a}{a+b+c}$=$\frac{2(a+b+c)}{a+b+c}$=2,
所以,k=2,
综上所述,k的值为2或-1.
故选C.
点评 本题考查了比例的性质,主要利用了等比性质,难点在于分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列方程中是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | (x-1)(x+2)=1 | C. | ax2+bx+c=0 | D. | x2-2x-3 |
2.在下列各数-$\frac{22}{7}$,0,1.5,-3,5$\frac{1}{2}$,50%,+8中,是整数的有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
9.钓鱼岛是中国的固有领土,位于中国东海,面积约4400000平方米,数据4400000用科学记数法表示为( )
| A. | 44×105 | B. | 4.4×106 | C. | 0.44×107 | D. | 4.4×105 |
19.下列各数在数轴上的位置是在-2的左边的是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
6. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=8,且AE:BE=1:4,则AB的长度为( )
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=8,且AE:BE=1:4,则AB的长度为( )
 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=8,且AE:BE=1:4,则AB的长度为( )
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=8,且AE:BE=1:4,则AB的长度为( )| A. | 10 | B. | 5 | C. | 12 | D. | 5$\sqrt{3}$ |
3.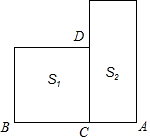 如图,若S1表示以BC为边的正方形面积,S2表示以AB为长、AC为宽的矩形面积,且S1=S2.则图中可看作线段黄金分割点的是( )
如图,若S1表示以BC为边的正方形面积,S2表示以AB为长、AC为宽的矩形面积,且S1=S2.则图中可看作线段黄金分割点的是( )
 如图,若S1表示以BC为边的正方形面积,S2表示以AB为长、AC为宽的矩形面积,且S1=S2.则图中可看作线段黄金分割点的是( )
如图,若S1表示以BC为边的正方形面积,S2表示以AB为长、AC为宽的矩形面积,且S1=S2.则图中可看作线段黄金分割点的是( )| A. | 点C | B. | 点D | C. | 点C和点D | D. | 没有 |
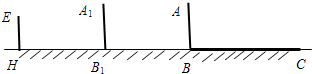 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.