题目内容
4.线段AB=4cm,点P为线段AB的黄金分割点,且AP>BP,则AP的长为(2$\sqrt{5}$-2)cm.分析 根据黄金分割点的定义和AP>BP得出AP=$\frac{\sqrt{5}-1}{2}$AB,代入数据即可得出AP的长度.
解答 解:由于P为线段AB=4的黄金分割点,
且AP>BP,
则AP=$\frac{\sqrt{5}-1}{2}$×4=(2$\sqrt{5}$-2)cm.
故答案为:(2$\sqrt{5}$-2)cm.
点评 本题考查了黄金分割.应该识记黄金分割的公式:较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$,较长的线段=原线段的$\frac{\sqrt{5}-1}{2}$.

练习册系列答案
相关题目
9.下列说法中,正确的是( )
| A. | 若|a|=a,则a=0 | B. | 角的两边越长,角的度数越大 | ||
| C. | 直线AB和直线BA是同一条直线 | D. | 多项式x3+x2的次数是5 |
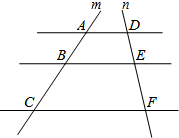 如图,直线AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=2,AC=5,DE=1.4,则DF的长为( )
如图,直线AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F.若AB=2,AC=5,DE=1.4,则DF的长为( )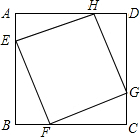 已知:如图,正方形ABCD的边长为1,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH也是正方形,设AE=x,正方形EFGH的面积为S.
已知:如图,正方形ABCD的边长为1,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH也是正方形,设AE=x,正方形EFGH的面积为S.