题目内容
19.化简(1)($\sqrt{2}$+$\sqrt{3}$)($\sqrt{2}$-$\sqrt{3}$)+$\frac{\sqrt{27}-\sqrt{12}}{\sqrt{3}}$.
(2)$\sqrt{40}$-5$\sqrt{\frac{1}{10}}$+$\sqrt{10}$.
分析 (1)根据平方差公式和二次根式的除法法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=2-3+$\sqrt{\frac{27}{3}}$-$\sqrt{\frac{12}{3}}$
=2-3+3-2
=0;
(2)原式=2$\sqrt{10}$-$\frac{\sqrt{10}}{2}$+$\sqrt{10}$
=$\frac{5\sqrt{10}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 假如小猫在如图所示的地板(图中每块方砖面积相等,小猫只停留在一块方砖上)上自由走动,它最终没有停在白色方砖上的概率为( )
假如小猫在如图所示的地板(图中每块方砖面积相等,小猫只停留在一块方砖上)上自由走动,它最终没有停在白色方砖上的概率为( )
 假如小猫在如图所示的地板(图中每块方砖面积相等,小猫只停留在一块方砖上)上自由走动,它最终没有停在白色方砖上的概率为( )
假如小猫在如图所示的地板(图中每块方砖面积相等,小猫只停留在一块方砖上)上自由走动,它最终没有停在白色方砖上的概率为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{9}$ | D. | $\frac{6}{9}$ |
8.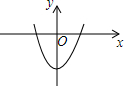 已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
 已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2-x+b=0根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法判断 |
9.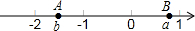 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
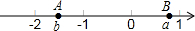 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
 如图,在矩形ABCD中,点E在AD上,EF⊥BE交CD于F,连接BF,则图中与△ABE一定相似的三角形是△DEF.
如图,在矩形ABCD中,点E在AD上,EF⊥BE交CD于F,连接BF,则图中与△ABE一定相似的三角形是△DEF.