题目内容
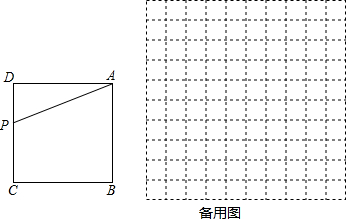
如图,在正方形ABCD中,AB=4,点P为线段DC上的一个动点.设DP=x,由点A,B,C,P首尾顺次相接形成图形的面积为y.
(1)求y关于x的函数表达式及x的取值范围;
(2)设(1)中函数图象的两个端点分别为M、N,且P为第一象限内位于直线MN右侧的一个动点,若△MNP正好构成一个等腰直角三角形,请求出满足条件的P点坐标;
(3)在(2)的条件下,若l为经过(-1,0)且垂直于x轴的直线,Q为l上的一个动点,使得S△MNQ=S△NMP,请直接写出符合条件的点Q的坐标.
(1)求y关于x的函数表达式及x的取值范围;
(2)设(1)中函数图象的两个端点分别为M、N,且P为第一象限内位于直线MN右侧的一个动点,若△MNP正好构成一个等腰直角三角形,请求出满足条件的P点坐标;
(3)在(2)的条件下,若l为经过(-1,0)且垂直于x轴的直线,Q为l上的一个动点,使得S△MNQ=S△NMP,请直接写出符合条件的点Q的坐标.

考点:一次函数综合题
专题:
分析:(1)根据梯形的面积公式,可得函数解析式,根据线段的和差,可得x的取值范围;
(2)根据等腰直角三角形的关系,可得方程组,根据解方程组,可得答案;
(3)根据等底等高的三角形面积相等,可得CD的长,根据勾股定理,可得方程组,根据解方程组,可得C点坐标.
(2)根据等腰直角三角形的关系,可得方程组,根据解方程组,可得答案;
(3)根据等底等高的三角形面积相等,可得CD的长,根据勾股定理,可得方程组,根据解方程组,可得C点坐标.
解答:解:(1)由线段的和差,得PC=(4-x),
由梯形的面积公式,得y=-2x+16
x的取值范围是0<x<4;
(2)设P点坐标是(a,b),M(0,16),N(4,8),
由△MNP正好构成一个等腰直角三角形,得
,化简,得
a=12-2b ③.
把③代入①得
5b2-48b+48=0.解得b=
,b=
(不符合题意要舍去),
a=12-2×
=
,
P点坐标是(
,
)
(3)由S△MNQ=S△NMP,得
CD=PN=4
.
过点C作CD⊥MN与D点,
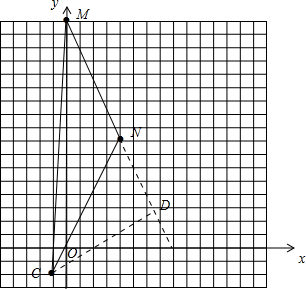
设点C的坐标为(-1,b),设ND=x,MD=4
+x,
由勾股定理,得
NC2-CD2=ND2,即(-1-4)2+(b-8)2-80=x2①,
MC2-CD2=MD2,即(-1)2+(b-16)2-80=(4
+x)2②,
②-①,得x=
,
把x=
代入①,得
b2-36b-76=0.解得b=38,b=-2,
C点坐标是(-1,-2),(-1,38).
由梯形的面积公式,得y=-2x+16
x的取值范围是0<x<4;
(2)设P点坐标是(a,b),M(0,16),N(4,8),
由△MNP正好构成一个等腰直角三角形,得
|
a=12-2b ③.
把③代入①得
5b2-48b+48=0.解得b=
24+4
| ||
| 5 |
24-4
| ||
| 5 |
a=12-2×
24+4
| ||
| 5 |
72-8
| ||
| 5 |
P点坐标是(
72-8
| ||
| 5 |
24+4
| ||
| 5 |
(3)由S△MNQ=S△NMP,得
CD=PN=4
| 5 |
过点C作CD⊥MN与D点,

设点C的坐标为(-1,b),设ND=x,MD=4
| 5 |
由勾股定理,得
NC2-CD2=ND2,即(-1-4)2+(b-8)2-80=x2①,
MC2-CD2=MD2,即(-1)2+(b-16)2-80=(4
| 5 |
②-①,得x=
| 11-2b | ||
|
把x=
| 11-2b | ||
|
b2-36b-76=0.解得b=38,b=-2,
C点坐标是(-1,-2),(-1,38).
点评:本题考查了一次函数综合题,(1)利用了梯形的面积公式,(2)利用等腰直角三角形的性质得出方程组是解题关键,(3)利用等底等高的三角形面积相等得出CD的长是解题关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长.
如图,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长.