题目内容
12. 如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.
如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.(1)若BC=4$\sqrt{2}$,CF=$\sqrt{17}$,求BF的长.
(2)若在(1)的条件下,求DE的长.
分析 (1)根据等腰直角三角形的性质求出OC、OB,根据勾股定理求出OF,计算即可;
(2)连接OE,根据切线的性质得到∠OED=90°,根据等腰三角形的性质求出DE=DF,根据切割线定理计算即可.
解答 解:(1)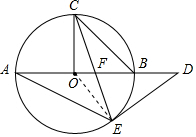 ∵CO⊥AB,
∵CO⊥AB,
∴OC=OB=$\frac{\sqrt{2}}{2}$BC=4,
∴OF=$\sqrt{C{F}^{2}-O{C}^{2}}$=1,
∴BF=OB-OF=3;
(2)连接OE,
∵DE与圆O相切于E,
∴∠OED=90°,
∴∠OEC+∠CED=90°,
∵∠OCF+∠OFC=90°,∠OFC=∠DFE,
∴∠DFE=∠DEF,
∴DF=DE,
由切割线定理得,DE2=DB•DA,
即DE2=(DE-3)(DE+5)
解得,DE=7.5.
点评 本题考查的是圆的切线的性质、切割线定理,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
相关题目
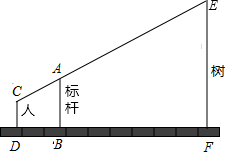 如图,竖立在点B处的标杆AB 长2.1米,某测量工作人员站在D点处,此时人眼睛C与标杆顶端A、树顶端E在同一直线上(点D、B、F也在同一直线上),已知此人眼睛与地面的距离CD 长1.6米,且BD=1米,BF=5米,求所测量树的高度.
如图,竖立在点B处的标杆AB 长2.1米,某测量工作人员站在D点处,此时人眼睛C与标杆顶端A、树顶端E在同一直线上(点D、B、F也在同一直线上),已知此人眼睛与地面的距离CD 长1.6米,且BD=1米,BF=5米,求所测量树的高度.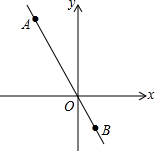 已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求:
已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求: 如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的角平分线.问:△ABC与△BDC相似吗?请说明理由.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的角平分线.问:△ABC与△BDC相似吗?请说明理由.