题目内容
20．
如图，在△ABC中，AB=AC，∠A=36°，BD是∠ABC的角平分线．问：△ABC与△BDC相似吗？请说明理由．
分析 先根据等腰三角形的性质得出∠ABC的度数，再由角平分线的性质得出∠CBD的度数，进而可得出结论．
解答 解：相似．
∵在△ABC中，AB=AC，∠A=36°，
∴∠ABC=$\frac{180°-36°}{2}$=72°．
∵BD是∠ABC的角平分线，
∴∠CBD=$\frac{1}{2}$∠ABC=36°，
∴∠CBD=∠A，∠C=∠C，
∴△ABC∽△BDC．
点评 本题考查的是相似三角形的判定，熟知有两组角对应相等的两个三角形相似是解答此题的关键．
练习册系列答案
相关题目
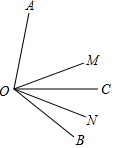如图，OM平分∠AOB，射线OC在∠BOM内部，ON是∠BOC的平分线．已知∠AOC=80°，那么∠MON的大小等于多少？
如图，D是直径AB延长线上一点，C是圆O上一点且CO⊥AB，连接CB，DE与圆O相切于E，EF与AB相交于F．
如图所示，把△ABC绕点C顺时针旋转35°得到△A′B′C′，A′B′交AC于点D，已知∠A′DC=90°，求∠A的度数．
如图，沿长方形ABCD的对角线AC对折，点B落在点E上，AE与CD交于F点，
