题目内容
11. 如图,△ABC是等边三角形,BC=4,以B点为原点,BC所在的直线为x轴,建立直角坐标系,则A点的坐标为(2,2$\sqrt{3}$).
如图,△ABC是等边三角形,BC=4,以B点为原点,BC所在的直线为x轴,建立直角坐标系,则A点的坐标为(2,2$\sqrt{3}$).
分析 过点A作AD⊥x轴于点D,利用含30度的直角三角形性质以及等边三角形的性质求出OB、AD的长度即可.
解答 解: 过点A作AD⊥x轴于点D,
过点A作AD⊥x轴于点D,
∵△OAC是等边三角形,
∴OA=OC=4,
由三线合一可知:OD=$\frac{1}{2}$OC=2,
由勾股定理可知:AD=2$\sqrt{3}$
∴点A的坐标为(2,2$\sqrt{3}$)
故答案为:(2,2$\sqrt{3}$)
点评 本题考查等边三角形的性质,解题的关键是熟练运用等边三角形的性质,以及勾股定理,本题属于基础基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若方程组$\left\{\begin{array}{l}{x+2y=1+m}\\{2x+y=3}\end{array}\right.$中,若未知数x,y满足x+y>0,则m的取值范围是( )
| A. | m≥-4 | B. | m>-4 | C. | m<-4 | D. | m≤-4 |
19.某废品收购站为了鼓励市民回收废品,如果一次回收2千克以上的废旧报纸,那么超过2千克部分的废旧报纸每千克比原价多付20%,根据下表,回答下列问题:
(1)回收1千克废旧报纸的价格是0.5元;
(2)设收购废旧报纸的质量为x千克,付款全额为y元,求y关于x的函数表达式;
(3)若小明在废品收购站卖废旧报纸一次性获得5.8元,那么他回收了多少废旧报纸?
| 回收废旧报纸的质量/千克 | 1.5 | 2 | 3.5 | 4 | … |
| 付款全额/元 | 0.75 | 1.0 | 1.9 | 2.2 | … |
(2)设收购废旧报纸的质量为x千克,付款全额为y元,求y关于x的函数表达式;
(3)若小明在废品收购站卖废旧报纸一次性获得5.8元,那么他回收了多少废旧报纸?
6.抛物线y=ax2-4ax-3a的对称轴是( )
| A. | 直线x=3 | B. | 直线x=2 | C. | 直线x=1 | D. | 直线x=-4 |
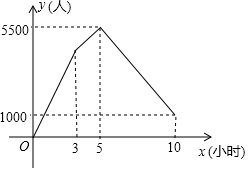 国家“5A”级景区某日迎来客流高峰,从索道开始运行前3小时开始,每小时都有a名游客源源不断地涌入候客大厅排队.索道每小时运送b名游客上山,索道运行2小时后,景区调来若干辆汽车和索道一起送游客上山,其中每小时有$\frac{7}{5}$b名游客乘坐汽车上山.5小时后,在候客大厅排队的游客人数降至1000人,候客大厅排队的游客人数y(人)与游客开始排队后的时间x(小时)之间的关系如图所示.则a=1500.
国家“5A”级景区某日迎来客流高峰,从索道开始运行前3小时开始,每小时都有a名游客源源不断地涌入候客大厅排队.索道每小时运送b名游客上山,索道运行2小时后,景区调来若干辆汽车和索道一起送游客上山,其中每小时有$\frac{7}{5}$b名游客乘坐汽车上山.5小时后,在候客大厅排队的游客人数降至1000人,候客大厅排队的游客人数y(人)与游客开始排队后的时间x(小时)之间的关系如图所示.则a=1500. 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.