题目内容
 如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F
如图,在△ABC中,AB=AC,以AB边为直径作⊙O,交BC边于点D,过点D作,DF⊥AC于点F(1)求证:DF为⊙O的切线;
(2)已知:⊙O的半径为5,DC=2
| 5 |
考点:切线的判定
专题:
分析:(1)求出OD和AC平行,推出OD垂直DF,根据切线的判定推出即可;
(2)根据勾股定理求出AD,根据三角形面积公式求出DF,根据勾股定理求出CF即可.
(2)根据勾股定理求出AD,根据三角形面积公式求出DF,根据勾股定理求出CF即可.
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵AO=BO,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∵OD为半径,
∴DF为⊙O的切线;
(2)解:连接AD,
∵:⊙O的半径为5,DC=2
,
∴BD=DC=2
,AB=2×5=10
在Rt△ADB中,由勾股定理得:AD=
=4
,
在Rt△ADC中,AB=AC=10,CD=2
,由三角形面积公式得:10×DF=4
×2
,
∴DF=4,
在Rt△DFCB中,CD=2
,DF=4,由勾股定理得:CF=
=2.
 (1)证明:连接OD,
(1)证明:连接OD,∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵AO=BO,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∵OD为半径,
∴DF为⊙O的切线;
(2)解:连接AD,
∵:⊙O的半径为5,DC=2
| 5 |
∴BD=DC=2
| 5 |
在Rt△ADB中,由勾股定理得:AD=
102-(2
|
| 5 |
在Rt△ADC中,AB=AC=10,CD=2
| 5 |
| 5 |
| 5 |
∴DF=4,
在Rt△DFCB中,CD=2
| 5 |
(2
|
点评:本题考查了切线的判定,圆周角定理,平行线的性质和判定,等腰三角形性质,相似三角形的性质和判定的应用,题目比较典型,是一定比较好的题目,难度适中.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.sin37°≈
小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.sin37°≈ 如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.
如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.
 如图,张明想用半径为r的圆形桌布将边长为60cm的正方形餐桌盖住,请你算一算这块圆形桌布的面积至少为多少时才能恰好盖住?(π取3.14)
如图,张明想用半径为r的圆形桌布将边长为60cm的正方形餐桌盖住,请你算一算这块圆形桌布的面积至少为多少时才能恰好盖住?(π取3.14)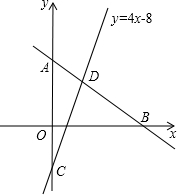 如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线y=4x-8与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积.
如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线y=4x-8与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积.