题目内容
20.在解方程ax2+bx+c=0(a≠0)时,甲由于抄错c的值,因而得出方程的两根分别为1与6,乙由于抄错b的值,因而得到的两根分别为-1和8,试求原来的方程,并解之.分析 由根与系数的关系可得1+6=-$\frac{b}{a}$,-1×8=$\frac{c}{a}$,得到b=-7a,c=-8a,进而求解即可.
解答 解:由题意得1+6=-$\frac{b}{a}$,-1×8=$\frac{c}{a}$,
则b=-7a,c=-8a,
所以原方程为ax2-7ax-8a=0,
∵a≠0,
∴原方程可化为x2-7x-8=0,
解得x1=-1,x2=8.
点评 本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了解一元二次方程.

练习册系列答案
相关题目
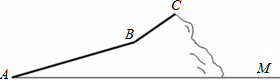 数学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为200$\sqrt{13}$米,斜坡BC的长为200$\sqrt{2}$米,坡度是1:1,已知A点海拔121米,C点海拔721米.
数学活动小组组织一次登山活动,他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为200$\sqrt{13}$米,斜坡BC的长为200$\sqrt{2}$米,坡度是1:1,已知A点海拔121米,C点海拔721米.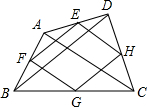 如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加AC=BD条件,就能保证四边形EFGH是菱形.
如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加AC=BD条件,就能保证四边形EFGH是菱形.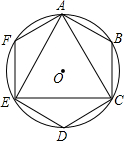 在等边△ACE内接于⊙O,连接B,D,F分别是$\widehat{AB}$,$\widehat{CE}$,$\widehat{AE}$的中点,连接AB,BC,CD,DE,EF,FA.将该图形绕点O旋转一个合适的角度后会与原图形重合,则这个旋转角的度数可能是( )
在等边△ACE内接于⊙O,连接B,D,F分别是$\widehat{AB}$,$\widehat{CE}$,$\widehat{AE}$的中点,连接AB,BC,CD,DE,EF,FA.将该图形绕点O旋转一个合适的角度后会与原图形重合,则这个旋转角的度数可能是( )