题目内容
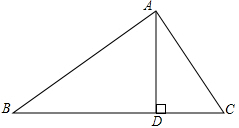 在△ABC中,AD⊥BC,tan∠B=cos∠CAD,求证:AC=BD.
在△ABC中,AD⊥BC,tan∠B=cos∠CAD,求证:AC=BD.考点:解直角三角形
专题:证明题
分析:由垂直的定义得到∠ADB=∠ADC=90°,在分别根据三角函数的定义得到tan∠B=
,cos∠CAD=
,根据题意得
=
,然后根据比例的性质即可得到结论.
| AD |
| BD |
| AD |
| AC |
| AD |
| BD |
| AD |
| AC |
解答:证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,tan∠B=
在Rt△ADC中,cos∠CAD=
,
∵tan∠B=cos∠CAD,
∴
=
,
∴AC=BD.
∴∠ADB=∠ADC=90°,
在Rt△ABD中,tan∠B=
| AD |
| BD |
在Rt△ADC中,cos∠CAD=
| AD |
| AC |
∵tan∠B=cos∠CAD,
∴
| AD |
| BD |
| AD |
| AC |
∴AC=BD.
点评:本题考查了解直角三角形:熟练掌握三角函数的定义.注意选择合适的直角三角形.

练习册系列答案
相关题目
小明家距学校m千米,一天他从家上学先以a千米/时的匀速跑步锻炼前进,后以匀速b千米/时步行到达学校,共用n小时.下图中能够反映小明同学距学校的距离s(千米)与上学的时间t(小时)之间的大致图象是( )
A、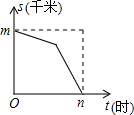 |
B、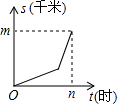 |
C、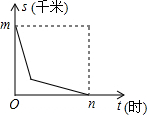 |
D、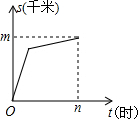 |
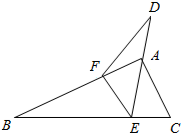 如图,一纸片△ABC中,AE平分∠BAC,将∠B对折至D,使其边BE的一部分与AE重合,折痕为EF,∠AEC=72°,∠DFA=8°,则∠C的度数为( )
如图,一纸片△ABC中,AE平分∠BAC,将∠B对折至D,使其边BE的一部分与AE重合,折痕为EF,∠AEC=72°,∠DFA=8°,则∠C的度数为( )| A、68° | B、72° |
| C、40° | D、80° |
 计算图中长方体的体积.
计算图中长方体的体积.
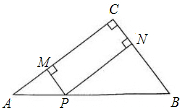 如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.
如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.