题目内容
、三角形的两边长分别为8和6，第三边的长是一元二次方程
的一个实数根，则该三角形的面积是多少？
解：首先解方程x2﹣16x+60=0得，
原方程可化为：（x﹣6）（x﹣10）=0，
解得x1=6或x2=10；
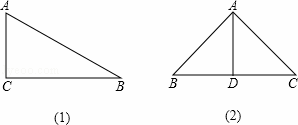
如图（1）根据勾股定理的逆定理，△ABC为直角三角形，
S△ABC=
×6×8=24；
如图（2）AD=
=
，
S△ABC=×8×2
=8
．
练习册系列答案
相关题目
题目内容
、三角形的两边长分别为8和6，第三边的长是一元二次方程的一个实数根，则该三角形的面积是多少？
解：首先解方程x2﹣16x+60=0得，
原方程可化为：（x﹣6）（x﹣10）=0，
解得x1=6或x2=10；
如图（1）根据勾股定理的逆定理，△ABC为直角三角形，
S△ABC=×6×8=24；
如图（2）AD==，
S△ABC=×8×2=8．