题目内容
三角形的两边长分别为10cm和17cm,第三条边上的高为8cm,则这个三角形的面积为
84或36
84或36
cm2.分析:本题考虑两种情况,一种为相邻两边在高的两侧,一种为相邻两边在高的同侧,然后根据勾股定理求得第三边,从而求得三角形面积.
解答:解:设AB=17cm,AC=10cm,AD=8cm,
由题意作图,有两种情况: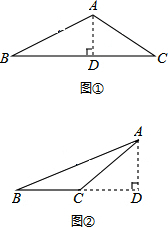
第一种:如图①,
在Rt△ABD中,利用勾股定理BD=6cm,CD=15cm,
∴BC=21cm,
∴三角形面积=
×BC•AD=84cm2,
第二种:如图②,
在Rt△ABD中,BD=15cm,
在Rt△ACD中,CD=6cm,
∴BC=BD-CD=9cm,
∴三角形面积=
×BC•AD=36cm2,
故答案为:84或36
由题意作图,有两种情况:

第一种:如图①,
在Rt△ABD中,利用勾股定理BD=6cm,CD=15cm,
∴BC=21cm,
∴三角形面积=
| 1 |
| 2 |
第二种:如图②,
在Rt△ABD中,BD=15cm,
在Rt△ACD中,CD=6cm,
∴BC=BD-CD=9cm,
∴三角形面积=
| 1 |
| 2 |
故答案为:84或36
点评:本题考查了勾股定理,两次运用勾股定理求出第三边,从两种情况来求第三边长,则再求三角形面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个直角三角形的两边长分别为3和4,则下列说法正确的是( )
| A、它的第三边一定为5 | ||
B、它的第三边一定为
| ||
C、它的第三边为5或
| ||
| D、它的第三边不能确定 |