题目内容
9.如果$\sqrt{x-3}$与|y+1|互为相反数,求x-y的平方根.分析 根据非负数的性质和题目中$\sqrt{x-3}$与|y+1|互为相反数,可以得到x、y的值,从而可以求得x-y的平方根.
解答 解:∵$\sqrt{x-3}$与|y+1|互为相反数,
∴x-3=0,y+1=0,
解得,x=3,y=-1,
∴$±\sqrt{x-y}=±\sqrt{3-(-1)}=±2$,
即x-y的平方根是±2.
点评 本题考查非负数的性质,解答本题的关键是明确非负数的性质,求出相应的x、y的值.

练习册系列答案
相关题目
17.若k≠0,b>0,则y=kx+b的图象可能是( )
| A. | 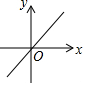 | B. | 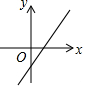 | C. | 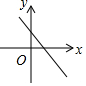 | D. | 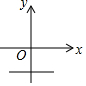 |
4.$\frac{2}{3}$sin60°的值等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
18.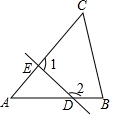 如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )
如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )
 如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )
如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为( )| A. | 130° | B. | 180° | C. | 230° | D. | 260° |

 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-1,2),C(-2,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-1,2),C(-2,1) 如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.
如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.


