题目内容
11．要将抛物线y=（x+1）2+2平移后得到抛物线y=x2，下列平移方法正确的是（ ）| A． | 向左平移1个单位，再向上平移2个单位 | |
| B． | 向左平移1个单位，再向下平移2个单位 | |
| C． | 向右平移1个单位，再向上平移2个单位 | |
| D． | 向右平移1个单位，再向下平移2个单位 |
分析 根据二次函数图象的平移规律进行解答．
解答 解：∵y=x2=（x+1-1）2+2-2，
∴抛物线y=x2可由y=（x+1）2+2向右平移1个单位，向下平移2个单位得出；
故选D．
点评 本题考查了二次函数图象的平移与几何变换，熟练掌握平移的规律：左加右减，上加下减是解题的关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
如图所示，在△ABC中，D是BC上一点，E，F，G，H分别是BD，BC，AC，AD的中点，请你探究EG，HF的位置关系，并说明理由．
2．
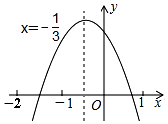如图是二次函数y=ax2+bx+c（a≠0）的图象，有下列结论：①ab＞0；②a+b+c＜0；③b+2c＜0；④a-2b+4c＞0；⑤a=$\frac{3}{2}$b．其中正确的有（ ）
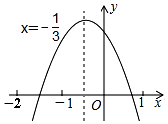如图是二次函数y=ax2+bx+c（a≠0）的图象，有下列结论：①ab＞0；②a+b+c＜0；③b+2c＜0；④a-2b+4c＞0；⑤a=$\frac{3}{2}$b．其中正确的有（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
19．以下选项是二次函数f（x）=x2+（m-3）x+1的图象与x轴的交点（x1，0）（x2，0）均在A（1，0）右侧的充要条件的是（ ）
| A． | $\left\{\begin{array}{l}f（1）＞0\\ \frac{3-m}{2}＞1\\△≥0\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x_1}+{x_2}＞2\\{x_1}{x_2}＞1\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}f（1）＞0\\ \frac{3-m}{2}＞2\\△＞0\end{array}\right.$ | D． | $\left\{\begin{array}{l}f（1）＜0\\△＞0\end{array}\right.$ |
6．函数y=$\frac{1}{x}$中自变量x的取值范围是（ ）
| A． | x≠1 | B． | x≠0 | C． | x＞0 | D． | 全体实数 |
16．下列各式成立的是（ ）
| A． | $\sqrt{9}=±3$ | B． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C． | $\sqrt{{{（-3）}^2}}=-3$ | D． | ${（-\sqrt{3}）^2}=3$ |
1．已知非零向量$\overrightarrow{a}$与$\overrightarrow{b}$，那么下列说法正确的是（ ）
| A． | 如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，那么$\overrightarrow{a}$=$\overrightarrow{b}$ | B． | 如果|$\overrightarrow{a}$|=|-$\overrightarrow{b}$|，那么$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C． | 如果$\overrightarrow{a}$∥$\overrightarrow{b}$，那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D． | 如果$\overrightarrow{a}$=-$\overrightarrow{b}$，那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| |