题目内容
20．若关于x的一元二次方程x2-2x+m-3=0有两个不相等的实数根，则m的取值范围是（ ）| A． | m＜-2 | B． | m＞4 | C． | m≤4 | D． | m＜4 |
分析 根据一元二次方程的根的判别式，建立关于m的不等式，求出m的取值范围即可．
解答 解：∵关于x的一元二次方程x2-2x+m-3=0有两个不相等的实数根，
∴△=b2-4ac=4-4×1×（m-3）＞0，
∴m＜4．
∴m的取值范围是m＜4；
故选D．
点评 此题考查了根的判别式，一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．
练习册系列答案
春雨教育同步作文系列答案
相关题目
10．
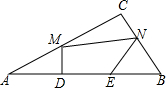如图，Rt△ABC中，∠C=90°，点D、E为边AB上的点，且AD=BE，点M、N分别为边AC、BC上的点，已知AB=a，DE=b，则四边形DMNE的周长的最小值为（ ）
如图，Rt△ABC中，∠C=90°，点D、E为边AB上的点，且AD=BE，点M、N分别为边AC、BC上的点，已知AB=a，DE=b，则四边形DMNE的周长的最小值为（ ）| A． | a | B． | 2a-b | C． | a+b | D． | a+2b |
11．以下列各组线段为边长，能构成直角三角形的是（ ）
| A． | 1，1，$\sqrt{3}$ | B． | 3，4，5 | C． | 5，10，13 | D． | 2，3，4 |
8．有一种推理游戏叫做“天黑请闭眼”，9位同学参与游戏，通过抽牌决定所扮演的角色，事先做好9张卡牌（除所写文字不同，其余均相同），其中有法官牌1张，杀手牌2张，好人牌6张．小易参与游戏，如果只随机抽取一张，那么小易抽到杀手牌的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{9}$ | D． | $\frac{1}{9}$ |
15．一个不透明的口袋中装有3个红球和12个黄球，这些球除了颜色外，无其他差别，从中随机摸出一个球，恰好是红球的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{5}$ | D． | $\frac{4}{5}$ |
5．
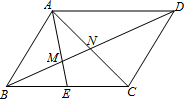如图，在?ABCD中，E为BC的中点，连接AE、AC，分别交BD于M、N，则BM：DN等于（ ）
如图，在?ABCD中，E为BC的中点，连接AE、AC，分别交BD于M、N，则BM：DN等于（ ）| A． | 1：2 | B． | 1：3 | C． | 2：3 | D． | 以上都不正确 |
12．
实数a，b在数轴上的位置如图所示，下列式子错误的是（ ）
实数a，b在数轴上的位置如图所示，下列式子错误的是（ ）| A． | a＞b | B． | -a＜-b | C． | ab＞0 | D． | a+b＞0 |