题目内容
13.已知一抛物线的顶点在原点,对称轴为y轴,且经过点(3,-3),则该抛物线的函数解析式为y=-$\frac{1}{3}$x2.分析 根据图象顶点为原点得到抛物线的c值为0,再由对称轴为y轴,得到b=0,设出适当的表达式,把(3,-3)代入设出的表达式中,求出a的值,即可确定出抛物线的表达式.
解答 解:∵抛物线的顶点在原点,对称轴是y轴,
∴设此抛物线的表达式是y=ax2,
把(3,-3)代入y=ax2中得:-3=9a,解得:a=-$\frac{1}{3}$,
则此抛物线的表达式是y=-$\frac{1}{3}$x2.
故答案为:y=-$\frac{1}{3}$x2.
点评 此题考查了待定系数法求二次函数的解析式,解答本题的关键是设出适当的解析式.

练习册系列答案
相关题目
2.下列计算错误的是( )
| A. | $\frac{{a}^{3}{b}^{2}}{{a}^{2}{b}^{3}}$=$\frac{a}{b}$ | B. | $\frac{(a-b)^{2}}{b-a}$=a-b | ||
| C. | $\frac{{m}^{2}-2m}{4-{m}^{2}}$=-$\frac{m}{m+2}$ | D. | $\frac{0.2a+b}{0.5a-b}$=$\frac{2a+10b}{5a-10b}$ |
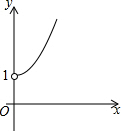
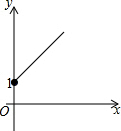
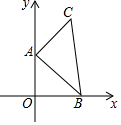 如图所示,点A的坐标为(0,1),点B是x轴上位于原点右侧的一个动点,以AB为直角边作Rt△ABC,使tan∠ABC=$\frac{3}{4}$,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图所示,点A的坐标为(0,1),点B是x轴上位于原点右侧的一个动点,以AB为直角边作Rt△ABC,使tan∠ABC=$\frac{3}{4}$,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )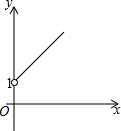
 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由. 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6. 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.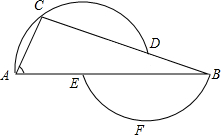 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,已知∠A=66°,试求∠B的度数.
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,已知∠A=66°,试求∠B的度数.