题目内容
18. 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.
分析 由反比例函数的图象过第一象限可得出k1>0,k2>0,再由反比例函数系数k的几何意义即可得出S△OAP=$\frac{1}{2}$k1,S△OBP=$\frac{1}{2}$k2,根据△OAB的面积为2结合三角形之间的关系即可得出结论.
解答 解:∵反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象均在第一象限内,
∴k1>0,k2>0.
∵AP⊥x轴,
∴S△OAP=$\frac{1}{2}$k1,S△OBP=$\frac{1}{2}$k2.
∴S△OAB=S△OAP-S△OBP=$\frac{1}{2}$(k1-k2)=3,
解得:k1-k2=6.
故答案为:6
点评 本题考查了反比例函数与一次函数的交点问题已经反比例函数系数k的几何意义,解题的关键是得出S△OAB=$\frac{1}{2}$(k1-k2).本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义用系数k来表示出三角形的面积是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
9.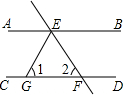 如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=40°,则∠1的度数是( )
如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=40°,则∠1的度数是( )
 如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=40°,则∠1的度数是( )
如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=40°,则∠1的度数是( )| A. | 70° | B. | 65° | C. | 60° | D. | 50° |
6.已知抛物线y=(m+1)x${\;}^{{m^2}+m}}$有最高点,则m的值是( )
| A. | m<-1 | B. | m=1 | C. | m=-2 | D. | m=1或m=-2 |
3.下列函数中,是二次函数的是( )
| A. | y=2x | B. | y=${x^2}+\frac{1}{x}$ | C. | y=$\sqrt{{x}^{2}-2x+1}$ | D. | y=x2-2 |
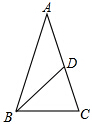 顶角为36°的等腰三角形称为黄金三角形(即:点D是AC的黄金分割点),如图,在△ABC中,AB=AC=1,∠A=36°,BD是三角形ABC的角平分线,那么AD=$\frac{\sqrt{5}-1}{2}$.
顶角为36°的等腰三角形称为黄金三角形(即:点D是AC的黄金分割点),如图,在△ABC中,AB=AC=1,∠A=36°,BD是三角形ABC的角平分线,那么AD=$\frac{\sqrt{5}-1}{2}$.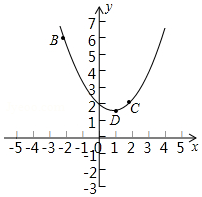 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.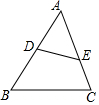 如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.
如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.