题目内容
绵州大剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数关系式;
(2)请计算并确定出最节省费用的购票方案.
(1)设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数关系式;
(2)请计算并确定出最节省费用的购票方案.
考点:一次函数的应用
专题:应用题
分析:(1)首先根据优惠方案①:付款总金额=购买成人票金额+除去4人后的学生票金额;
优惠方案②:付款总金额=(购买成人票金额+购买学生票金额)×打折率,列出y关于x的函数关系式,
(2)根据(1)的函数关系式求出当两种方案付款总金额相等时,购买的票数.再就三种情况讨论.
优惠方案②:付款总金额=(购买成人票金额+购买学生票金额)×打折率,列出y关于x的函数关系式,
(2)根据(1)的函数关系式求出当两种方案付款总金额相等时,购买的票数.再就三种情况讨论.
解答:解:(1)按优惠方案①可得
y1=20×4+(x-4)×5=5x+60(x≥4),
按优惠方案②可得
y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1-y2=0.5x-12(x≥4),
①当y1-y2=0时,得0.5x-12=0,解得x=24,
∴当购买24张票时,两种优惠方案付款一样多.
②当y1-y2<0时,得0.5x-12<0,解得x<24,
∴4≤x<24时,y1<y2,优惠方案①付款较少.
③当y1-y2>0时,得0.5x-12>0,解得x>24,
当x>24时,y1>y2,优惠方案②付款较少.
y1=20×4+(x-4)×5=5x+60(x≥4),
按优惠方案②可得
y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1-y2=0.5x-12(x≥4),
①当y1-y2=0时,得0.5x-12=0,解得x=24,
∴当购买24张票时,两种优惠方案付款一样多.
②当y1-y2<0时,得0.5x-12<0,解得x<24,
∴4≤x<24时,y1<y2,优惠方案①付款较少.
③当y1-y2>0时,得0.5x-12>0,解得x>24,
当x>24时,y1>y2,优惠方案②付款较少.
点评:本题根据实际问题考查了一次函数的运用.解决本题的关键是根据题意正确列出两种方案的解析式,进而计算出临界点x的取值,再进一步讨论.

练习册系列答案
相关题目
若x是实数,已知M=3x2-5x+2,N=2x2-3x+1,则M,N的大小关系是( )
| A、M>N | B、M<N |
| C、M=N | D、M≥N |
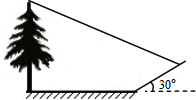 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.