题目内容
5.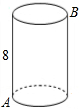 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )cm.
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )cm.| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 此题最直接的解法就是将圆柱展开,然后利用两点之间线段最短解答.
解答  解:底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为:$\frac{1}{2}$×2π×$\frac{6}{π}$=6(cm),展开得:
解:底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为:$\frac{1}{2}$×2π×$\frac{6}{π}$=6(cm),展开得:
∵BC=8cm,AC=6cm,
根据勾股定理得:AB=$\sqrt{{8}^{2}+{6}^{2}}$=10(cm).
故选C.
点评 此题考查的是平面展开-最短路径问题,解题的关键是根据题意画出展开图,表示出各线段的长度,再利用勾股定理求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.将-6-(+3)-(-7)+(-2)中的减法改成加法并写成省加号的和的形式是( )
| A. | -6-3+7-2 | B. | 6-3-7-2 | C. | 6-3+7-2 | D. | 6+3-7-2 |
20.下列说法中,正确的是( )
| A. | 三角形的角平分线是射线 | |
| B. | 三角形的高总在三角形的内部 | |
| C. | 一个三角形的三个内角中至少有一个直角 | |
| D. | 三角形的中线一定在三角形的内部 |
10. 如图,点A、B、C在⊙O上,且∠AOB=90°,则∠C的度数为( )
如图,点A、B、C在⊙O上,且∠AOB=90°,则∠C的度数为( )
 如图,点A、B、C在⊙O上,且∠AOB=90°,则∠C的度数为( )
如图,点A、B、C在⊙O上,且∠AOB=90°,则∠C的度数为( )| A. | 22.5° | B. | 30° | C. | 45° | D. | 60° |