题目内容
15.(1)已知等腰三角形的一边等于6cm,一边等于7cm,求它的周长;(2)已知等腰三角形的一边长为5cm,周长为20cm,求其它的边长.
分析 (1)分6是等腰三角形的腰长与底边两种情况讨论求解;
(2)已知条件中,本题没有明确说明已知的边长是否是腰长,所以有两种情况讨论,还应判定能否组成三角形.
解答 解:(1)①6是腰长时,周长=6+6+7=19;
②6是底边时,7是腰,周长=6+7+7=20;
综上,它的周长为19或20;
(2)①底边长为5,则腰长为:(20-5)÷2=7.5,所以另两边的长为7.5cm,7.5cm,能构成三角形;
②腰长为5,则底边长为:20-5×2=10,底边长为10cm,另一个腰长为5cm,不能构成三角形.
因此另两边长为7.5cm、7.5cm.
点评 考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
6. 如图,△ABC沿直线AB平移得到△DEF下面结论中,错误的是( )
如图,△ABC沿直线AB平移得到△DEF下面结论中,错误的是( )
 如图,△ABC沿直线AB平移得到△DEF下面结论中,错误的是( )
如图,△ABC沿直线AB平移得到△DEF下面结论中,错误的是( )| A. | △ABC≌△DEF | B. | ∠A=∠D | C. | AC=DE | D. | EF=BC |
10.已知三角形的两边长为4,8,则第三边的长度可以是( )
| A. | 16 | B. | 8 | C. | 4 | D. | 1 |
20.计算:$(-1)÷(-7)×(-\frac{1}{7})$的结果是( )
| A. | -1 | B. | 1 | C. | $-\frac{1}{49}$ | D. | -49 |
7.大于-2.7而小于1.5的所有整数的乘积是( )
| A. | 0 | B. | -2 | C. | 2 | D. | -1 |
4.$\frac{3}{4}$,-$\frac{5}{6}$,-$\frac{7}{8}$的大小顺序是( )
| A. | -$\frac{7}{8}$<-$\frac{5}{6}$<$\frac{3}{4}$ | B. | -$\frac{7}{8}$<$\frac{3}{4}$<-$\frac{5}{6}$ | C. | -$\frac{5}{6}$<-$\frac{7}{8}$<$\frac{3}{4}$ | D. | $\frac{3}{4}$<-$\frac{5}{6}$<-$\frac{7}{8}$ |
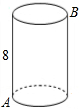 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )cm.
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )cm. 如图,△ABC和△DEF中,AC、DF相交于点G,且AG=DG,FG=CG,BF=CE,点B、F、C、E在同一直线上.求证:∠B=∠E.
如图,△ABC和△DEF中,AC、DF相交于点G,且AG=DG,FG=CG,BF=CE,点B、F、C、E在同一直线上.求证:∠B=∠E.