题目内容
5. 如图,四边形ABCD中,AB∥CD,点F是BC的中点,EF∥AB,连接DF并延长与AB的延长线交于点G,若AB:CD=3:1,EF=8cm,则CD的长是4cm.
如图,四边形ABCD中,AB∥CD,点F是BC的中点,EF∥AB,连接DF并延长与AB的延长线交于点G,若AB:CD=3:1,EF=8cm,则CD的长是4cm.
分析 直接利用相似三角形的判定与性质得出△DEF∽△DAG,△DCF∽GBF,进而得出AG的长,再利用全等三角形的性质得出BG=DC求出答案即可.
解答 解:∵AB∥CD,EF∥AB,
∴△DEF∽△DAG,△DCF∽GBF,
∵点F是BC的中点,
∴DF=FG,$\frac{EF}{BG}$=$\frac{1}{2}$,
∴△DCF≌GBF,
∴BG=DC,
∵AB:CD=3:1,EF=8cm,
∴AG=16cm,
∴BG=$\frac{1}{4}$×16=4(cm),
∴CD=4cm.
故答案为:4.
点评 此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质,正确得出AG的长是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
15.在一个口袋中有5个除颜色外完全相同的小球,其中有3个黄球,1个黑球,1个白球,从中随机摸出一个小球,则摸到黄球的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
13.点P(2,-3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17. 如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )
如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )
 如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )
如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |

 如图,两圆圆心相同,大圆的弦AB与小圆相切,若图中阴影部分的面积是16π,则AB的长为8.
如图,两圆圆心相同,大圆的弦AB与小圆相切,若图中阴影部分的面积是16π,则AB的长为8.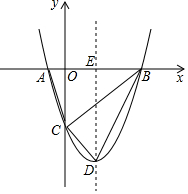 如图,抛物线与x轴交于A,B两点,点B坐标是(3,0),与y轴交于点C,顶点D的坐标是(1,-4),对称轴与x轴交于点E
如图,抛物线与x轴交于A,B两点,点B坐标是(3,0),与y轴交于点C,顶点D的坐标是(1,-4),对称轴与x轴交于点E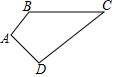 已知在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.
已知在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.