题目内容
10. 如图,两圆圆心相同,大圆的弦AB与小圆相切,若图中阴影部分的面积是16π,则AB的长为8.
如图,两圆圆心相同,大圆的弦AB与小圆相切,若图中阴影部分的面积是16π,则AB的长为8.
分析 设AB与小圆切于点C,连结OC,OB,根据圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2)=16π,即可求解.
解答  解:如图所示:设AB与小圆切于点C,连结OC,OB.
解:如图所示:设AB与小圆切于点C,连结OC,OB.
∵AB与小圆切于点C,
∴OC⊥AB,
∴BC=AC=$\frac{1}{2}$AB.
∵圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2)=16π,
又∵直角△OBC中,OB2=OC2+BC2
∴圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2)=π•BC2=16π,
∴BC=4,故AB=2BC=8.
故答案为:8.
点评 此题考查了垂径定理,切线的性质以及勾股定理,解题的关键是正确作出辅助线,注意到圆环(阴影)的面积=π•OB2-π•OC2=π(OB2-OC2),利用勾股定理把圆的半径之间的关系转化为直角三角形的边的关系.

练习册系列答案
相关题目
18.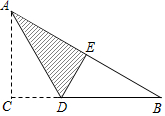 如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )| A. | x2=(8-x)2+62 | B. | x2=(8-x)2+42 | C. | x=8-x+4 | D. | x2=62+82 |

 如图,四边形ABCD中,AB∥CD,点F是BC的中点,EF∥AB,连接DF并延长与AB的延长线交于点G,若AB:CD=3:1,EF=8cm,则CD的长是4cm.
如图,四边形ABCD中,AB∥CD,点F是BC的中点,EF∥AB,连接DF并延长与AB的延长线交于点G,若AB:CD=3:1,EF=8cm,则CD的长是4cm.

 如图,AB为半圆O的直径,C为半圆上一点,∠AOC=60°,点P在AB的延长线上,且PB=BO=3cm.连接PC交半圆于点D,过P作PE⊥PA交AD的延长线于点E,求PE长.
如图,AB为半圆O的直径,C为半圆上一点,∠AOC=60°,点P在AB的延长线上,且PB=BO=3cm.连接PC交半圆于点D,过P作PE⊥PA交AD的延长线于点E,求PE长.