题目内容
16.已知在数轴上有A,B两点,点A表示的数为8,点B在A点的左边,且AB=12.若有一动点P从数轴上点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿着数轴向右匀速运动,设运动时间为t秒.(1)解决问题:①当t=1秒时,写出数轴上点B,P所表示的数;
②若点P,Q分别从A,B两点同时出发,问点P运动多少秒与Q相距3个单位长度?
(2)探索问题:若M为AQ的中点,N为BP的中点.当点P在P、Q上运动过程中,探索线段MN与线段PQ的数量关系(写出过程).

分析 (1)①根据已知可得B点表示的数为8-12;点P表示的数为8-3t;
②点P运动x秒时,与Q相距2个单位长度,则AP=3x,BQ=2x,根据AP+BQ=AB-3,或AP+BQ=AB+3,列出方程求解即可;
(2)根据点P在点A、B两点之间运动,故MN=MQ+NP-PQ,由此可得出结论.
解答 解:(1)①∵点A表示的数为8,B在A点左边,AB=12,
∴点B表示的数是8-12=-4,
∵动点P从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,
∴点P表示的数是8-3×1=5.
②设点P运动x秒时,与Q相距3个单位长度,
则AP=3x,BQ=2x,
∵AP+BQ=AB-3,
∴3x+2x=9,
解得:x=1.8,
∵AP+BQ=AB+3,
∴3x+2x=15
解得:x=3.
∴点P运动1.8秒或3秒时与点Q相距3个单位长度.
(2)2MN+PQ=12或2MN-PQ=12;理由如下:
P在Q右侧时有:MN=MQ+NP-PQ=$\frac{1}{2}$AQ+$\frac{1}{2}$BP-PQ=$\frac{1}{2}$(AQ+BP-PQ)-$\frac{1}{2}$PQ=$\frac{1}{2}$AB-$\frac{1}{2}$PQ=$\frac{1}{2}$(12-PQ),
即2MN+PQ=12.
同理P在Q左侧时有:2MN-PQ=12.
点评 本题考查了数轴和一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.下列各式计算正确的是( )
| A. | 2a+3b=5ab | B. | 3a2-2a2=a2 | C. | 5a2b-3ab2=2a2b | D. | 3a-(2a-b)=a-b |
4.一种药品经过两次降价,药价从每盒60元下调至每盒48.6元,则平均每次降价的百分比是( )
| A. | 1% | B. | 10% | C. | 1.9% | D. | 19% |
8. 某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)样本容量是50,并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.
 某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:(1)样本容量是50,并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.
| 组别 | 课堂发言次数n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
 如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.已知DG=a,BG=b,CG=2GH且a、b满足下列关系:a2+b2=5,ab=2,
如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.已知DG=a,BG=b,CG=2GH且a、b满足下列关系:a2+b2=5,ab=2,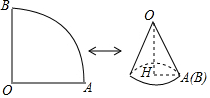 如图,已知扇形AOB的圆心角为90°,面积为16π.
如图,已知扇形AOB的圆心角为90°,面积为16π. 如图,四边形ABCD中,AB∥CD,点F是BC的中点,EF∥AB,连接DF并延长与AB的延长线交于点G,若AB:CD=3:1,EF=8cm,则CD的长是4cm.
如图,四边形ABCD中,AB∥CD,点F是BC的中点,EF∥AB,连接DF并延长与AB的延长线交于点G,若AB:CD=3:1,EF=8cm,则CD的长是4cm.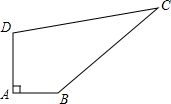 如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四边形ABCD的面积.
如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四边形ABCD的面积.