题目内容
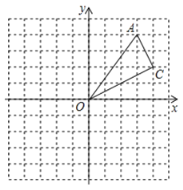
【题目】如图,![]() 中,
中,![]() ,在
,在![]() 上截取
上截取![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于
于![]() 。
。
(1)若![]() 为
为![]() 的中点,
的中点,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.

【答案】(1)![]() ;(2)解解析.
;(2)解解析.
【解析】
(1)先证明△ABC为等边三角形,得到AB=BD=4,进而求得BE=2,在Rt△EBF中,∠EBF=60°,得到∠BEF=30°,求出BF=![]() BE=1.再利用勾股定理即可解答;
BE=1.再利用勾股定理即可解答;
(2)取FM=BF,由EF⊥BM,BF=FM,知BE=EM=CD,再证明△EMH≌△CDH,得到DH=HM,从而FH=FM+MH=BF+DH=![]() BE+DH.
BE+DH.
(1)∵∠A=60°,AD=AB,
∴△ABC为等边三角形,
∴AB=BD=4,
∵E为AB的中点,
∴BE=2,
在Rt△EBF中,∠EBF=60°,
∴∠BEF=30°
∴BF=![]() BE=1.
BE=1.
∴EF=![]() .
.
(2)如图,取FM=BF,由EF⊥BM,BF=FM,知BE=EM=CD,

又∵∠BEF=∠FEM=30°,
∴∠BEM=∠A=60°,
∴EM∥AC,
∴∠MEH=∠HCD,∠EHM=∠CHD,
在△EMH和△CDH中,
 ,
,
∴△EMH≌△CDH,
∴DH=HM,
∴FH=FM+MH=BF+DH=![]() BE+DH.
BE+DH.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目