题目内容
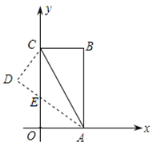
【题目】如图![]() ,矩形
,矩形![]() 的一边落在矩形
的一边落在矩形![]() 的一边上,并且矩形
的一边上,并且矩形![]() ,其相似比为
,其相似比为![]() ,连接
,连接![]() 、
、![]() .
.

![]() 试探究
试探究![]() 、
、![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
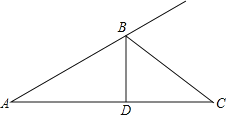
![]() 将矩形
将矩形![]() 绕着点
绕着点![]() 按顺时针(或逆时针)旋转任意角度
按顺时针(或逆时针)旋转任意角度![]() ,得到图形
,得到图形![]() 、图形
、图形![]() ,请你通过观察、分析、判断
,请你通过观察、分析、判断![]() 中得到的结论是否能成立,并选取图
中得到的结论是否能成立,并选取图![]() 证明你的判断;
证明你的判断;
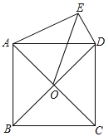
![]() 在
在![]() 中,矩形
中,矩形![]() 绕着点
绕着点![]() 旋转过程中,连接
旋转过程中,连接![]() 、
、![]() 、
、![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
【答案】(1) ![]() ,理由详见解析;(2)
,理由详见解析;(2)![]() 仍然成立,理由详见解析;(3)
仍然成立,理由详见解析;(3)![]() 的面积是否存在最大值与最小值,
的面积是否存在最大值与最小值,![]() ,
,![]() .
.
【解析】
(1)由矩形CEFG~矩形CDAB可以得出∠BCD=∠DCE=90°,![]() ,从而可以得到△BCG∽△DCE,再利用角相等通过代换就可以得出结论;
,从而可以得到△BCG∽△DCE,再利用角相等通过代换就可以得出结论;
(2)由条件可以得出证明△BCG∽△DCE,再利用角相等通过代换就可以得出结论;
(3)矩形CEFG绕着点C旋转一周,点F的轨迹是以点C为圆心以![]() 为半径的圆,所以△BDF的BD边上的高就是点F到BD的距离,也就是BD到圆上的点的距离,有最大值和最小值,最大值为点C到BD的距离与圆的半径的和,最小值为点C到BD的距离与圆的半径的差,再利用三角形的面积公式求解即可.
为半径的圆,所以△BDF的BD边上的高就是点F到BD的距离,也就是BD到圆上的点的距离,有最大值和最小值,最大值为点C到BD的距离与圆的半径的和,最小值为点C到BD的距离与圆的半径的差,再利用三角形的面积公式求解即可.
(1)![]() ,理由如下:
,理由如下:
如图![]() ,∵矩形
,∵矩形![]() 矩形
矩形![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
延长![]() 交
交![]() 于
于![]() .
.
又∵![]() ,
,
∴![]() ,
,

∴![]() ;
;
(2)![]() 仍然成立,理由如下:
仍然成立,理由如下:
如图![]() ,∵矩形
,∵矩形![]() 矩形
矩形![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(3)![]() 的面积是否存在最大值与最小值.理由如下:
的面积是否存在最大值与最小值.理由如下:
∵矩形![]() ,其相似比
,其相似比![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
设点![]() 到
到![]() 的距离为
的距离为![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴当点![]() 到
到![]() 的距离为
的距离为![]() 时,
时,![]() 的面积有最大值,
的面积有最大值,
当点![]() 到
到![]() 的距离为
的距离为![]() 时,
时,![]() 的面积有最小值,
的面积有最小值,
![]() ,
,
![]() .
.

练习册系列答案
相关题目