题目内容
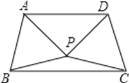
【题目】如图，四边形
内接于
，
为直径，
平分
，与
相交于
．
求证：
；
若直径
，
，求
的值．
【答案】(1)详见解析;(2)
．
【解析】
（1）证△CBE∽△DBC，得出比例式，即可得出答案；
（2）求出△ACB是等腰直角三角形，求出BC，根据（1）和已知求出BE、DE，根据相交弦定理求出即可．
（1）∵BD平分∠ADC，∴∠ADB=∠CDB．
∵∠ADB=∠ECB，∴∠BDC=∠BCE．
∵∠DBC=∠CBE，∴△CBE∽△DBC，∴
=
，∴BC2=BEBD．
（2）∵∠ADB=∠CDB，∠ADB=∠ACB，∠CDB=∠CAB，∴∠ACB=∠BAC，∴AB=BC．
∵AC为直径，∴∠ABC=90°，∴△ABC为等腰直角三角形．在Rt△ABC中，∠ABC=90°，AB=BC，AC=6
，由勾股定理得：BC=6．
∵BC2=BEBD，BE：ED=3：1，∴设ED=x，则BE=3x，BD=4x，∴36=12x2，解得：x=
，设OE=y，则AE=3+y，CE=3﹣y．
由相交弦定理得：（3+y）（3﹣y）=3，解得：y=3，即OE=3．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
