题目内容
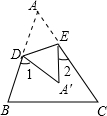 如图,将∠A=50°的△ABC的∠A沿直线DE折叠,则∠1+∠2=( )
如图,将∠A=50°的△ABC的∠A沿直线DE折叠,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、130° |
考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:根据将∠A=50°的△ABC的∠A沿直线DE折叠,得出∠ADE=∠EDA′,∠AED=∠DEA′,再利用∠A+∠ADE+∠AED=180°,
得出∠ADE+∠AED=180°-50°=130°,进而求出∠1+∠2=360°-2(∠ADE+∠AED)得出答案即可.
得出∠ADE+∠AED=180°-50°=130°,进而求出∠1+∠2=360°-2(∠ADE+∠AED)得出答案即可.
解答:解:∵将∠A=50°的△ABC的∠A沿直线DE折叠,
∴∠ADE=∠EDA′,∠AED=∠DEA′,
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-50°=130°,
∴∠1+∠2=360°-2(∠ADE+∠AED)=360°-2×130°=100°.
故选:B.
∴∠ADE=∠EDA′,∠AED=∠DEA′,
∵∠A+∠ADE+∠AED=180°,
∴∠ADE+∠AED=180°-50°=130°,
∴∠1+∠2=360°-2(∠ADE+∠AED)=360°-2×130°=100°.
故选:B.
点评:此题主要考查了折叠问题与三角形内角和定理,利用折叠前后图形不发生任何变化,得出∠ADE=∠EDA′,∠AED=∠DEA′是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知反比例函数y=
已知反比例函数y=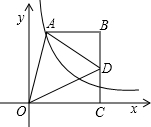 如图,点A在双曲线y=
如图,点A在双曲线y=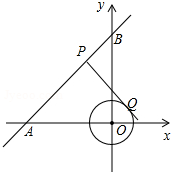 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )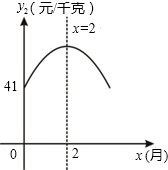 已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示:
已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示: 某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).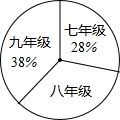 “读书好,读好书,好读书.”阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.为了培养学生的读书习惯,某校组织学生开展“绿色大阅读”活动.右图是在活动之初某校对三个年级学生信息做的一个调查.图1是人数分布扇形统计图,其中八年级人数为408人,表2是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
“读书好,读好书,好读书.”阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.为了培养学生的读书习惯,某校组织学生开展“绿色大阅读”活动.右图是在活动之初某校对三个年级学生信息做的一个调查.图1是人数分布扇形统计图,其中八年级人数为408人,表2是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题: