题目内容
 已知反比例函数y=
已知反比例函数y=| k |
| 2x |
考点:反比例函数综合题
专题:综合题
分析:把过一次函数的两个点代入一次函数,即可求得k,进而求得反比例函数的解析式,因为A点同时在这两个函数解析式上,让这两个函数组成方程组求解即可得到A点坐标,然后求出OA的距离,再根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
解答: 解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
,
解得k=2,
∴反比例函数解析式为y=
;
将y=
和一次函数y=2x-1组成方程组得
,
解得
,
,
∵点A在第一象限,
∴点A的坐标为(1,1).
∴OA=
=2,OA与x轴所夹锐角为45°,
①当OA为腰时,由OA=OP1得P1(
,0),
由OA=OP2得P2(-
,0);
由OA=AP3得P3(2,0).
②当OA为底时,OP4=AP4得P4(1,0).
∴符合条件的点有4个,分别是(
,0),(-
,0),(2,0),(1,0).
故答案为(
,0),(-
,0),(2,0),(1,0).
 解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
解:将(a,b)、(a+1,b+k)分别代入一次函数y=2x-1解析式得
|
解得k=2,
∴反比例函数解析式为y=
| 1 |
| x |
将y=
| 1 |
| x |
|
解得
|
|
∵点A在第一象限,
∴点A的坐标为(1,1).
∴OA=
| 12+12 |
①当OA为腰时,由OA=OP1得P1(
| 2 |
由OA=OP2得P2(-
| 2 |
由OA=AP3得P3(2,0).
②当OA为底时,OP4=AP4得P4(1,0).
∴符合条件的点有4个,分别是(
| 2 |
| 2 |
故答案为(
| 2 |
| 2 |
点评:本题考查了反比例函数的相关问题,在这条直线上的各点的坐标一定适合这条直线的解析式.同时在两个函数解析式上,应是这两个函数解析式的公共解.答案较多时,应有规律的去找不同的解.

练习册系列答案
相关题目
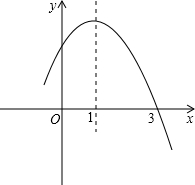 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其中对称轴为:x=1,则下列4个结论中正确的结论有( )个
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其中对称轴为:x=1,则下列4个结论中正确的结论有( )个①abc<0;②a+c>b;③2a+3b>0;④a+b>am2+bm(m≠1);⑤c<-2a.
| A、2个 | B、3个 | C、4个 | D、5个 |
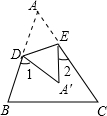 如图,将∠A=50°的△ABC的∠A沿直线DE折叠,则∠1+∠2=( )
如图,将∠A=50°的△ABC的∠A沿直线DE折叠,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、130° |
 正比例函数y1=k1x与反比例函数y2=
正比例函数y1=k1x与反比例函数y2= 已知:如图,△ABC、直线m、点M在网格中如图所示的位置,请按以下要求作图:
已知:如图,△ABC、直线m、点M在网格中如图所示的位置,请按以下要求作图: 粗心的小马在画数轴时只标了单位长度(一格表示单位长度为1)和正方向,而忘了标上原点(如图),若点B和点C点表示的两个数的绝对值相等,则点A表示的数是
粗心的小马在画数轴时只标了单位长度(一格表示单位长度为1)和正方向,而忘了标上原点(如图),若点B和点C点表示的两个数的绝对值相等,则点A表示的数是