题目内容
10.已知M=$\root{a-b}{a+b+3}$是a+b+3的算术平方根,N=$\root{a-2b+3}{a+2b}$是a+2b的立方根,求18N-M2的立方根.分析 根据算术平方根和立方根的定义得出关于a、b的方程组,求出a、b的值,求出M、N的值,最后代入求出18N-M2的值,根据立方根的定义求出即可.
解答 解:∵M=$\root{a-b}{a+b+3}$是a+b+3的算术平方根,N=$\root{a-2b+3}{a+2b}$是a+2b的立方根,
∴$\left\{\begin{array}{l}{a-b=2}\\{a-2b+3=3}\end{array}\right.$,
解方程组得:a=4,b=2,
∴M=$\sqrt{9}$=3,N=$\root{3}{8}$=2,
∴18N-M2=27,
∴18N-M2的立方根是3.
点评 本题考查了立方根,算术平方根,解二元一次方程组的应用,解此题的关键是求出M、N的值,难度不是很大.

练习册系列答案
相关题目
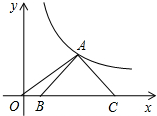 如图,等腰Rt△ABC的底边BC在x轴上,顶点A在双曲线y=$\frac{3}{x}$(x>0)上,连接OA,则OC2-OA2=( )
如图,等腰Rt△ABC的底边BC在x轴上,顶点A在双曲线y=$\frac{3}{x}$(x>0)上,连接OA,则OC2-OA2=( ) 在?ABCD中,两条对角线AC与BD相交于点O,BC=5,AC=6,BD=8,求△AOB的周长.
在?ABCD中,两条对角线AC与BD相交于点O,BC=5,AC=6,BD=8,求△AOB的周长.