题目内容
1．
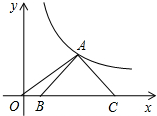如图，等腰Rt△ABC的底边BC在x轴上，顶点A在双曲线y=$\frac{3}{x}$（x＞0）上，连接OA，则OC2-OA2=（ ）| A． | 6 | B． | 4 | C． | 3 | D． | 2 |
分析 设A（a，$\frac{3}{a}$），过点A作AD⊥x轴于点D，根据等腰三角形的性质用a表示出AD=BD=DC=$\frac{3}{a}$，再表示出OC及OA的长，进而得出结论．
解答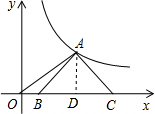 
解：设A（a，$\frac{3}{a}$），过点A作AD⊥x轴于点D，
∵△ABC是等腰直角三角形，
∴OD=a，AD=BD=DC=$\frac{3}{a}$，OC=a+$\frac{3}{a}$，
∴OC2-OA2=（a+$\frac{3}{a}$）2-【a2+（$\frac{3}{a}$）2】=6．
故选A．
点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
6．下面有六个汽车标志图案，其中是轴对称图形有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
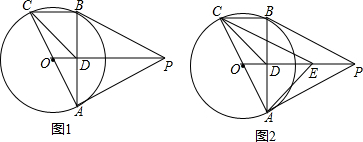
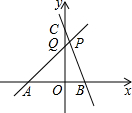如图，在平面直角坐标系xOy中，已知直线PA是一次函数y=x+m（m＞0）的图象，直线PB是一次函数y=-3x+n（n＞m）的图象，点P是两直线的交点，点A、B、C、Q分别是两条直线与坐标轴的交点．若四边形PQOB的面积是5.5，且CQ：AO=1：2，若存在一点D，使以A、B、P、D为顶点的四边形是平行四边形，则点D的坐标为（$\frac{13}{2}$，$\frac{9}{2}$）或（-$\frac{11}{2}$，$\frac{9}{2}$）或（-$\frac{5}{2}$，-$\frac{9}{2}$）．