题目内容
14.如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC,AB=5,DE=1,BD=8,设CD=x.(1)直接写出AC+CE的值;(用含x的代数式表示)
(2)求AC+CE的最小值.

分析 (1)根据线段的和差,可得BC的长,根据勾股定理,可得答案;
(2)根据两点之间线段最短,可得线段AC+CE的最小值=AE,根据勾股定理,可得答案.
解答 解:(1)由线段的和差,得
BC=(8-x).
由勾股定理,得
AC+CE=$\sqrt{A{B}^{2}+B{C}^{2}}$+$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{{5}^{2}+(5-x)^{2}}$+$\sqrt{1+{x}^{2}}$=$\sqrt{(8-x)^{2}+25}$+$\sqrt{{x}^{2}+1}$;
(2)如图,作CF⊥AB于F点.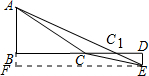 ,
,
四边形BDEF是矩形,
BF=DE=1,EF=BD=8,
AF=AB+BF=5+1=6,
AC+CE的最小值=AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
点评 本题考查了轴对称-最短路线问题,(1)利用勾股定理;(2)利用两点之间线段最短得出C1的位置是解题关键.

练习册系列答案
相关题目
 如图所示,作出△ABC关于直线l的对称三角形A'B'C'.
如图所示,作出△ABC关于直线l的对称三角形A'B'C'.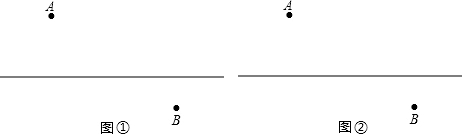
 如图,已知数轴上有A、B、C三个点,它们表示的数分别是a、b和8,O是原点,且(a+20)2+|b+10|=0.
如图,已知数轴上有A、B、C三个点,它们表示的数分别是a、b和8,O是原点,且(a+20)2+|b+10|=0. 如图,请至少写出4对同旁内角.
如图,请至少写出4对同旁内角.